1916211-Advanced Power System Simulation Laboratory

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

DEPARTMENT OF ELECTRICAL & ELECTRONICS ENGINEERING

LAB MANUAL / OBSERVATION

SRM VALLIAMMAI ENGINEERING COLLEGE

1916211 – ADVANCED POWER SYSTEM SIMULATION LABORATORY

Regulation 2019

Academic Year 2019-2020 Even

M.E (POWER SYSTEMS ENGINEERING)

Prepared By

V.SUDHAGAR,AP(Sr.G)/EEE

(An Autonomous Institution)

SRM Nagar, Kattankulathur

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

SYLLABUS

1. Small-signal stability analysis of single machine-infinite bus system using classical

machine model

2. Small-signal stability analysis of multi-machine configuration with classical machine model

3. Induction motor starting analysis

4. Load flow analysis of two-bus system with STATCOM

5. Transient analysis of two-bus system with STATCOM

6. Available Transfer Capability calculation using an existing load flow program

7. Study of variable speed wind energy conversion system- DFIG

8. Study of variable speed wind energy conversion system- PMSG

9. Computation of harmonic indices generated by a rectifier feeding a R-L load

10. Design of active filter for mitigating harmonics.

1916211 – ADVANCED POWER SYSTEM SIMULATION LABORATORY

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

CYCLE - I

1. Small-signal stability analysis of single machine-infinite bus system using classical

machine model

2. Small-signal stability analysis of multi-machine configuration with classical machine model

3. Induction motor starting analysis

4. Load flow analysis of two-bus system with STATCOM

5. Transient analysis of two-bus system with STATCOM

CYCLE – II

6. Available Transfer Capability calculation using an existing load flow program

7. Study of variable speed wind energy conversion system- DFIG

8. Study of variable speed wind energy conversion system- PMSG

9. Computation of harmonic indices generated by a rectifier feeding a R-L load

10. Design of active filter for mitigating harmonics.

ADDITIONAL EXPERIMENTS

1. Transient stability analysis SMIB using classical model

2. Small signal stability analysis of a single machine infinite bus system with field circuit,

exciter and power system stabilizer

1916211- ADVANCED POWER SYSTEM SIMULATION LABORATORY

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

INDEX

S.No

Date of

Experiment.

Name of the experiment

Date of

submission.

Staff Sign

10.

11.

12.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

EXP NO: 1 DATE:

SMALL–SIGNAL STABILITY ANALYSIS OF SINGLE-MACHINE-

INFINITE BUS(SMIB) SYSTEM

AIM:

To write a MATLAB program for analyzing the small-signal stability of a single-machine-

infinite bus system, assuming classical model of the generator (constant voltage behind transient

reactance)

THEORY:

Power system stability may be broadly defined as that property of a power system that

enables it to remain in a state of operating equilibrium under normal operating conditions and to

regain an acceptable state of equilibrium after being subjected to a disturbance

Power system stability may be broadly classified as (i) rotor angle stability and (ii) voltage

stability. Rotor angle stability is the ability of interconnected synchronous machines of a power

system to remain in synchronism.

Rotor angle stability can be further classified in to Transient stability and small signal

stability depending on the type of disturbance. Transient stability is the rotor angle stability study

of a system following large disturbances.

Small signal (or small disturbance) stability is the ability of the power system to maintain

synchronism under small disturbances. The disturbances are considered sufficiently small for

linearization of system equations to be permissible for purpose of analysis. Instability that may

result can be of two forms.

I. Steady increase in rotor angle due to lack of sufficient synchronizing torque.

II. Rotor oscillations of increasing amplitude due to lack of sufficient damping torque.

There are four modes of oscillations causing small signal instability in a power system. They are:

 Local Modes or Machine System Modes are associated with the swinging of units at a

generating station with respect to the rest of the power system. The frequency range of

oscillation is (0.8 to 2) Hz.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

 Inter area Modes are associated with the swinging of many machines in one part of the

system against machines in other parts. The frequency range for inter area modes is (0.2 to

0.8) Hz.

 Control Modes are associated with generating units and other controls.

 Torsional Modes are associated with the turbine-generator shaft system rotational

components.

Numerical Example :

The test system considered for small signal stability analysis is the single machine infinite

bus system from kundur (1994).

Fig.1. Single line diagram of SMIB system

Figure shows the system representation applicable to thermal generating station consist of

four 555MVA,24kV, 60Hz units.

The network reactances shown in the figure are in per unit on 2220MVA,24kV base

(referred to the LT side of the step-up transformer).Resistances are assumed to be

negligible.

The post fault system condition in per unit on the 2220MVA,24kV base is as

follows

P=0.9 Q=0.3(over excited) Et=1.0 36° E

=0.995∟0°

The generators are to be modeled as a single euivalenct generator represedted by the

classical model with the following parameters expressed in per unit of 2220 MVA 24kV

base

=0.3 H=3.5MW-s/MVA

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

(a) Write the linerarzed state equation of the system. Determine the eigen values, damped

frequency of oscillation in Hz, damping ratio and un damped natural frequency for each

of the following values of damping coefficient ( in pu torque/pu speed)

(i) K

=0 (ii) K

= -10.0 (iii) K

=10.0

(b) For the case with K

=-10.0 find the lift and right eigen vectors and participation matrix.

Determine the time response if at t=0 Δδ =5° and Δɷ=0

Generator Represented by Classical Model:

With the generator represented by the classical model and all resistances neglected the system

representation is as shown Fig.2.



Fig.2. Generator represented by classical model connected to the infinite bus

is the voltage behind

. Let δ be the angle by which

leads the infinite bus voltage

With

as reference phasor,

E E

  



(1)

 

E E cos jsin

   



(2)

The complex power behind

is given by

' ' ' *

S P jQ E I  

(3)

 

' ' '

B B

E E sin jE E E cos

   



(4)

With stator resistance neglected, the air gap power (P

) is equal to the terminal power (P). In per

unit, the air gap torque is equal to the air gap power.

Hence

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

E E sin

T P



 

(5)

Linearizing about an initial operating condition represented by

  

yields

E E sin





   



(6)

The equations of motion (from chapter 3 of Kundur) in per unit are

 

r m e D r

p T T K

    

0 r

p   

(7)

Where



is the per unit speed deviation,



is the rotor angle in electrical radians,



is the base

rotor electrical speed in rad/sec, and p is differential operator with time t in seconds.

Linearizing the above equations and substituting for

e s

T K  

we get,

 

r m e D r

p T T K

      

0 r

p   

(8)

r r

2H 2H



 

 

   

 

  

   

 

 

   



 

(9)

This is of the form

X Ax Bu 

(10)

The block diagram of the SMIB system for small signal analysis is shown in Fig.3.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Fig.3. Block diagram of the SMIB system with classical generator model

The natural frequency of oscillation of the swing modes is given by

n s



 

rad/s

& the damping ratio of the electro mechanical modes (swing modes) is

D D

s 0

K K

1 1

2 2H 2

k 2H

   

 

   



   

= synchronizing torque coefficient in p.u torque/ rad and

damping torque coefficient in

p.u of torque/p.u of speed deviation, H=inertia constant on MW-sec/MVA.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

FLOW CHART:

Read the load flow data

P,Q,H,E

,freq,

E ,K ,

gen dynamic

data

Calculate initial conditions

 

t t

I conj P jQ / E 

' '

t d t

E E jX *I 

 

s B 0 T

K abs E *abs E *cos / abs(X ) 

Linearize the system differential equations

Compute the matrix A

A = [

K / 2H

;



]

START

Compute the Eigen values, Eigen vectors (left &

right), participation matrix, undamped natural

frequency, damping ratio, plots (delta vs. time &

freq vs. time)

STOP

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Program:

clc;

p=0.9;

q=0.3;

et=1.0;

anget=0.628;

eb=0.995;

angeb=0;

xd=.3*i;

f=60;

xtr=.15*i;

x1=.5*i;

x2=.93*i;

h=input('enter the value of inertia');

fault=input('enter the line no:');

if fault==1

xt=xd+xtr+x2;

else

xt=xd+xtr+x1;

end

it=conj((p+q*i)/et);

edas=et+(xd*it);

angedas=angle(edas);

delta=anget+angeb+angedas;

ks=(edas*eb*cos(delta))/xt;

kd=input('enter the value of kd');

A=[-kd/(2*h) -abs(ks)/(2*h); (2*pi*f) 0]

lambda=eig(A)

[v d]=eig(A)

l=inv(v)

p=abs(v.*1)

s2=det(A);

wn=sqrt(s2);

f=sqrt(s2)/(2*pi)

s1=-(-kd/(2*h))+0;

zita=s1/(2*wn)

wd=wn*(sqrt(1-(zita*zita)));

wdh=wd/(2*pi)

%for plots using zero input response

th=acos(zita);

t=0:01:3;

dd=anget/sqrt(1-zita^2)*exp(-zita*wn*t).*sin(wd*t+th);

d=(delta+dd)*180/pi;

%relatie to synchronouly revolving feild

dw=-wn*anget/sqrt(1-zita^2)*exp(-zita*wn*t).*sin(wd*t);

ff=f+dw;

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

subplot(2,1,1),plot(t,d),grid

xlabel('t sec'),ylabel('delta degree')

subplot(2,1,2),plot(t,ff),grid

xlabel('t sec'),ylabel('rotor speed')

Output:

CASE-1: After the clearance of fault on line-1

CASE-2:

After the clearance of fault on line-2

INERTIA

CONSTANT,H

EIGEN

VALUES



(rad/sec)

DAMPING

RATIO



(Hertz)

3.5

0 + 6.3866i

0 - 6.3866i

6.3866

1.0165

-0.7143 + 6.3465i

-0.7143 - 6.3465i

6.3866

-0.1118

1.0165

INERTIA

CONSTANT,H

EIGEN

VALUES



(rad/sec)

DAMPING

RATIO



(Hertz)

3.5

0 + 4.3028i

0 - 4.3028i

4.3028

0.6848

-0.7143 + 4.2431i

-0.7143 - 4.2431i

4.3028

-0.1660

0.6848

-10

0.7143 + 4.2431i

0.7143 - 4.2431i

4.3028

0.1660

0.6848

7.0

0 + 3.0425i

0 - 3.0425i

3.0425

0.4842

-0.3571 + 3.0215i

-0.3571 - 3.0215i

3.0425

-0.1174

0.4842

-10

0.3571 + 3.0215i

0.3571 - 3.0215i

3.0425

0.1174

0.4842

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

-10

0.7143 + 6.3465i

0.7143 - 6.3465i

6.3866

0.1118

1.0165

7.0

0 + 4.5160i

0 - 4.5160i

4.5160

0.7187

-0.3571 + 4.5019i

-0.3571 - 4.5019i

4.5160

-0.0791

0.7187

-10

0.3571 + 4.5019i

0.3571 - 4.5019i

4.5160

0.0791

0.7187

(i) K

= 0

(ii) K

= 10

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

(iii) K

= -10

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

INFERENCE:

An increase in damping torque coefficient K

increases the damping ratio, whereas an

increase in inertia constant decreases both ω

and

ϛ.

RESULTS:

A MATLAB program was written to analyze the small-signal stability of a single-machine-

infinite bus (SMIB) system.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

EXP NO: 2 DATE:

SMALL SIGNAL STABILITY ANALYSIS OF MULTI-MACHINE SYSTEM

AIM:

To write a MATLAB program to analyze the small signal stability of a multi-machine

power system.

THEORY:

To analyze the small signal stability of the multi machine power system it is necessary to

reduce the original network to the size of the generators and to derive the equations for multi-

machine system that represent the dynamics of the machine and the controllers, in the state-space

form. The state variables for the machine are,  and possibly  and . The controllers of

the synchronous machine and the network will throw in additional state variables. The synchronous

machines are represented by constant voltage sources in series with their transient reactances.

Analysis methodology:

Step-1: Equations in network coordinates:

1i,1i 1i,1 1

2i,2i 2i,2 2

1,1i 11 12 1

2,2i 21 22 2

ˆ ˆ ˆ

Y 0 Y 0 0 .... E

ˆ ˆ ˆ

0 Y 0 Y 0 .... E

ˆ ˆ ˆ ˆ

Y 0 Y Y .... .... V

ˆ ˆ ˆ ˆ

0 Y Y Y .... .... V

0 0 .... .... .... .... .

.... .... .... .... .... .... .

  



  



  

 

  



 



 



 



 



 





 

 



(1)

In the above equation



and



are interval voltage phasors and



and



are the stator currents.

GG G,NG

NG,G NG,NG

Y Y

 



 



 

 

(2)

Where

G – Generator, NG – Non-generator.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

(a) Representation

(a) With generators and loads replaced by their equivalents

(b) All nodes except generator internal nodes eliminated

Fig1. Two machine n-bus system

1i,1i

2i,2i

Y 0

Y ;

0 Y

 



 

 

1i,1

G,NG

2i,2

Y 0 0 0 ....

Y ;

0 Y 0 0 ....

 



 

 

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

NG,G G,NG

Y Y ;

Dimension: (n-2)×2

11 12 13

21 22 23

NG,NG

31 32 33

Y Y Y .... ....

Y ;

Y Y Y .... ....

.... .... .... .... ....

 

 



 

 

Dimension: (n-2) × (n-2)

Step-2: Reduction of network equations:

Eliminate the non-generator nodes.

From Eq. (2), we get

NG NG.NG NG,G G

V Y {Y E }





 

(3)

Substituting Eq. (3) in Eq. (2), we get

red

G G

Y E I





(4)

Where

red 1

GG GG G,NG NG,NG NG,G

Y Y Y Y Y



 

(5)

With Eq. (4) step-2 is completed.

Step-3: Transformation of reduced equations:

Let and and and be the internal voltage and stator current phasors in individual

machine q-d coordinates. The corresponding quantities in network coordinates are , and , .

1 2

1 1

j j

1 1r 2 2r

j j

1 1r 2 2r

E E e ;E E e ;

I I e ;I I e ;

 

   

 

(6)



Relative displacements of q-axis of the machine with respect to the network

REF

The above relationships between the quantities in network and individual machine rotor

coordinates can be expressed as

G Gr G Gr

E TE ;I TI

 

 

(7)

Where T is the transformation matrix given by

j 2

e 0

0 e



 



 

 

(8)

and the subscript r denotes individual machine rotor coordinates.

The inverse transformation is given by

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

j 2

e 0

0 e

 



 

 



 

 

(9)

Gr Gr

I ME

(10)

1 red

M T Y T





(11)

11 12 12

12 12 22

j j( )

11 12

j( ) j

12 22

Y e Y e

  

  

 



 

 

(12)

Step-4: Linearization of reduced network equations in individual machine rotor coordinates:

Let us denote the relative displacements of individual machine q-axis with respect to network

reference as

1 10 1 2 20 2

; ;         

(13)

Let these incremental changes cause incremental changes in other quantities as follows:

I I I  

(14)

E E E

  

  

(15)

M M M  

(16)

T T T  

(17)

0 0 0 0 0

I I M E M E ME M E

   

         

(18)

0 0

I M E ME

 

    

(19)

Equation (19) represents the linearised reduced network equations in individual machine rotor

coordinates.

0 0 0 0

I M E j{ M M }E

 

      

(20)

12 12,0

12 12 22

j( )

11 12

j( ,0) j

12 22

Y e Y e

 



  

 



 

 

(21)

I

12,0 13,0 12,0

12,0 23,0 12,0 23,0

13,0 23,0

j j j

j ,0

11 q1 12 q2 13 q3 12 q20 12 13 q30 13

j j j j

12 q1 22 q2 23 q3 12 q10 12 23 q30 23

j j

13 q1 23 q2

Y E Y e E Y e E jY e E jY e E

Y e E Y E Y e E jY e E jY e E

Y e E Y e E

    

 

     

 

    

       

    

        

 

   

13,0 23,0

j j

33 q3 13 q10 13 23 q20 23

Y E jY e E jY e E

 

 

 

  

    

 

 

(22)

We can separate out the real and imaginary parts and obtain the q and d components.

Step-4 is now completed.

Step-5: Linearization of differential equations:

The acceleration equation for the machine given below:

 

i mi ei D i

2H T T K ,i 1,2



      

(23)

The above equation involves . We can easily shown that is a function of , and .

Assuming a 2-pole machine, the electrical power output in p.u. is given by

 

ˆ ˆ

P Re VI





In the individual machine q-d coordinates

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

   

 

e q d q d d d q q e

P Re V jV I jI V I V I T     

(24)

Assuming type 1B machine

   

 

e q q d d d q q

d q q d q q

T X I I X I E I

X X I I E I

 

   

 

  

(25)

Linearising Eq. (25),

 

e d q q0 d d0 q q0 q q0 q

T X X I I I I E I I E

  

 

         

 

(26)

i.e.

   

e q0 d q d0 q d q q0 d q0 q

T E X X I I X X I I I E

 

   

         

 

(27)

Equation (26) holds good for machine 1 or machine 2.

Hence,

   

e1 q10 d1 q1 d10 q1 d1 q1 q10 d1 q10 q1

T E X X I I X X I I I E

 

   

         

 

(27)

and

   

e2 q20 d2 q2 d20 q2 d2 q2 q20 d2 q20 q2

T E X X I I X X I I I E

 

   

         

 

(28)

Linearization of swing equation is straight forward. Linearization yields,

 

s i

,i 1,2



   

(29)

Linearising the differential equation for the voltage behind the transient reactance of machine-1 is

given by

 

q1 q1 d1 d1 d1 FD1

d01

p E E X X I E

  

 

        

 



(30)

Similarly, for the second machine we have

 

q2 q2 d2 d2 d2 FD2

d02

p E E X X I E

  

 

        

 



(31)

Equations (23) taken together with Eqs. (29), (30) and (31) are the linearised differential equations

required for small signal stability analysis. This completes step-5.

Step-6: Elimination of the incremental changes in algebraic variables from the linearised

differential equations:

e1 11 q1 12 q2 13 12

T T E T E T

 

      

(32)

e2 21 q1 22 q2 23 12

T T E T E T

 

      

(33)

The only equations that are to be expressed in the standard state variable form are the equations for

the incremental changes in the generator internal voltages.

q1 11 q1 12 q2 13 12 FD

d01

p E E E E E E E

  

        



(34)

Where

 

11 11 d1 d1

d01

E 1 B X X



   

 

 



(35)

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

 

12 d1 d1 12 12,0 12 12,0

d01

E X X B cos G sin



    



(36)

 

13 d1 d1 12 12,0 12 12,0 q20

d01

E X X G cos B sin E

 

     



(37)

Similarly for the second generator, we can show that

q2 21 q1 22 q2 23 12 FD2

d02

p E E E E E E E

  

        



(38)

Where

 

21 d2 d2 12 12,0 12 12,0

d02

E X X B cos G sin



    



(39)

 

22 22 d2 d2

d01

E 1 B X X



   

 

 



(40)

 

23 d2 d2 12 12,0 12 12,0 q10

d02

E X X G cos B sin E

 

     



(41)

m1 m2

1 2

13 23

D 11 21 12 22

12 12

1 3 1 2 1 2

12 12

q1 q1

d01

13 11 12

q2 q2

23 21 22

T T

2H 2H

T T

K T T T T

2H 2H 2H 2H 2H 2H 2H

0 0 0

p E E

0 E E E

p E E

0 E E E

 



 

 

   

 

     

   

 

 

   

   

   

 

 

 

   

 

 



 

   

 



 



   

 

 

 

   

   

 

 

FD2

d02

 

 



 



 

completed step-6

We can now apply eigenvalue analysis to the computed state space model.

Simplifications for classical machines:

Let us assume machine-1&2 are classical (Type 0). Note the following:

i. & are constant.  will be absent in the equation. Set all the terms

containing  to zero. Equation (27) for the incremental electrical torque becomes

e1 12 q2 13 12

T T E T    

(42)

ii. Set =

iii. The state variables are  ,  . Hence, only the equations for these variables are

to be considered.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Two identical machine feed a common load, the impedance between each machine

terminal 0+j0.8p.u on the total rated MVA, the terminal voltages of each machine is 1p.u

assume classical moadel for machine.

Generator data: Both generators are identical rating of each is 80MVA. Reactance

parameters X

=3.4p.u X

=0.49p.u Xq=3.28p.u T

=6 sec. Total kinetic energy stored at

synchrouns speed both machine 3979.2 MJ rated frequency=60Hz.

Load data: Both generators are identically loaded active power output of each machine

is 0.5p.u on totoal MVA power factor=0.851.Choose base MVA as 160

(i) Determine the network equations in the individual machine stator dq coordinates of small

signal stability analysis

(ii) Lineraised network equations in the individual machine rotor equation

(iii)Numerical expression for electrical torque

(iv)Eigen value and natural frequency

(i) E

´and E

q2´

are constant. ΔEq

´ will be absent in the equation, Set all the terms

containing E

´to zero. The incremental electrical torque becomes

ΔT

ΔEq

´+T

Δδ

(ii) Set X

d1´

(iii) The state variables are Δ

. ΔE

Hence only the equations for these

variable are to be considered.

To obtain the state matrix equations for this case ignore the third row and the third column

of the state matrix. If both machines are classical, then the state matrix obtained by ignoring the

third and fourth rows and third and fourth columns of the state matrix.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

PROGRAM:

%program for multimachine

clc;

clear all;

%program for multimachine

Et=1.0;

xd=3.4;

xdp=.49;

xq=3.28;

Td0p=6.0;

f=60;

rating=80;

kenergy=379.2;

xt=0.8;

%generator dataa

ngen=2;

%loading data

p1=0.5;

%0n total rated mva

p2=.5;

pf=.85;

basemva=160;

%initial loading conditions

b=acos(pf);

q1=p1*tan(b);

q2=q1;

s=p1+q1*i;

I1=s'/Et;

%stator current

I2=I1;

%voltage behind transient reactance

Eq1p=Et+(xdp*i)*(I1);

Eq2p=Eq1p;

delt10=angle(Eq1p);

delt20=angle(Eq2p);

%load current

IL=I1+I2;

%load voltage

vL=Et-xt*i*I1;

%load admittance

yL=IL/vL;

zL=1/yL;

a=real(zL);

b=imag(zL);

d=xdp+xt;

linedata=[1 3 0 d 0

3 2 0 d 0

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

0 3 a b 0];

i=sqrt(-1);

nl=linedata(:,1);

nr=linedata(:,2);

R=linedata(:,3);

X=linedata(:,4);

Bc=j*linedata(:,5);

nbr=length(linedata(:,1));

nbus=max(max(nl),max(nr));

Z=R+j*X;

y=ones(nbr,1)./Z;

%branch admittance

Ybus=zeros(nbus,nbus);

%initialize Ybus to Zero

%formation of the off diagonal elements

for k=1:nbr

if nl(k)>0 & nr(k)>0

Ybus(nl(k),nr(k))=Ybus(nl(k),nr(k))-y(k);

Ybus(nr(k),nl(k))=Ybus(nl(k),nr(k));

end

%formation of the diagonal elements

for n=1:nbus

for k=1:nbr

if nl(k)==n | nr(k)==n

Ybus(n,n)=Ybus(n,n)+y(k)+Bc(k);

end

Ybus

%COMPUTATION OF REDUCED Y BUS

ygg=Ybus(1:ngen,1:ngen);

ygl=Ybus(1:ngen,ngen+1:nbus);

ylg=Ybus(ngen+1:nbus,1:ngen);

yll=Ybus(ngen+1:nbus,ngen+1:nbus);

YBUS=ygg-ygl*inv(yll)*ylg;

%reduced Y bus

%network equations in individual machine qd coordinates

m=[0 1;1 0];

M=m.*YBUS;

Ep=[abs(Eq1p);abs(Eq2p)];

M0=M*Ep;

dI=[-1*i;1*i].*M0;

%numerical exp for elec torque

Eq10p=abs(Eq1p);

Eq20p=abs(Eq2p);

B12=imag(YBUS(1,2));d120=0;

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

T13=B12*cos(d120)*Eq10p*Eq20p

T23=-T13;

H1=kenergy/(2*80*2);

H2=H1;

a11=0;

a12=-((T13/(2*H1))-(T23/(2*H2)))

a21=2*pi*f;

a22=0;

A=[a11 a12;

a21 a22]

eig(A)

wn=sqrt(det(A))

fn=wn/(2*pi)

EIGEN VALUE ANALYSIS:

For P = 0.9; Q = 0.3; K

FOR CLASSICAL MODEL:

EIGEN VALUES

±9.7333i

DAMPING RATIO

FREQUENCY (HZ)

1.5491

INFERENCE:

From the damping ratio (=0) of the swing mode it can be observed that the system is small

signal unstable.

RESULT:

A MATLAB program was written to analyze the small-signal stability of a multi-machine

power system.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

EXP NO: 3 DATE:

INDUCTION MOTOR STARTING ANALYSIS

AIM:

To analyse the study of motor starting

THEORY:

The purpose of the motor starting is to determine the initial voltage depressions on the

distribution buses serving the motors and to calculate the approximate acceleration times of the

selected motors during starting-up. This information is used in determining if satisfactory motor

starting and acceleration will occur, if the protective devices are properly applied, and if the voltage

dips during starting will result in loss of adjacent loading due to contactor drop out.

A motor starting study should be made if the motor horse power exceeds approximately

30% of supply transformer(s) base KVA rating, if no generators are present. If generation is present

and no other sources are involved, a study should be considered whenever the motor horse power

exceeds 10-15% of the generator KVA rating

System modeling:

A simplified model of the distribution system is adapted. It contains the motor bus, the

associated main (typically 6.6 kV) bus and the main upstream higher voltage bus (typically 33 kV)

as shown in the single line diagram.

Equations:

Assume a base power for the system and that all the impedances shown are converted to the

base power. Let S

sys

be the system base power.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Equivalent circuit diagram

sys

Z p.u





 

 

 

(1)

Where, S



= 3-phase fault level at bus-2.

= Z

– transformer impedance converted to S

sys.

3 3

L L

Z p.u

P jQ





(2)

Where, Z

= Impedance of constant impedance loads in p.u

= Voltage of bus-3 in p.u

= Active power consumed by the load in p.u on S

sys

= Reactive power consumed by the load in p.u on S

sys

(+ve i/p)

= Impedance of capacitor, computed from reactive power injected at nominal voltage.

Z p.u





(3)

Where, Q

= Reactive power consumed by the capacitor in p.u on S

sys.

(-ve i/p)

BUS-2, V2

BUS-3, V3

Rtr

BUS-1, V1

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

= Impedance presented by the motor to the bus. At the instant of starting, it is equal to locked

rotor impedance of motor-Z

. It is a function of speed (and time) indirectly since motor current,

voltage and power factor are functions of speed (and time) during acceleration.

 

LR FL

Z e

I I





(4)

= Locked rotor impedance of motor in p.u on motor base.

Where,

= Locked rotor current in amp at rated voltage

= Full load current



= Starting power factor

3 3

3 M L C

Z Z / /Z / /Z

(5)

T I 

(6)

I lb ft s

  

(7)

2 2

0 0

2 ( )rev / s       

(8)

t t rev

    

(9)

T 2g

rev / s

 

(10)

A simplified approximation for starting time,

1 2

WK (rpm rpm )2

t(s)

60gT

 



(11)

Where, T – Average motor shaft output torque

v – Motor terminal voltage

– Moment of inertia

g – Acceleration due to gravity

 – Angular velocity

α – Angular acceleration

t – Time in seconds to accelerate

– Net average or accelerating torque between rpm-1 and rpm-2

θ – Electrical angle in degrees

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

– Inertia

Alternatively, if moment of inertia J is given in kg-m

acc

J T







acc

t J



 

(12)

t will be in seconds if  is in rad /sec

acc motor load

T T T 

Instantaneous torque,

1 2

2 2

s 1 2 1 2

q V (r s)

[(r (r s)) (x x ) ]



   

(13)

Where,

– Number of phases



– Angular velocity at synchronous speed

v – Motor terminal voltage

, x

– Stator resistance and reactance

, x

– Rotor resistance and reactance

s – Slip

In metric system, following are the consistent set of units for various quantities.

T, T

– Newton-meter

J – kg-m

replaces WK

/2g = I

 – Radians /sec

θ, θ – radians

Algorithm for advancing simulation to cover a speed interval:

Consider k-th interval

1) Read the value of I

inrush

from speed vs. current curve and 

from speed vs. power factor

curve. Calculate Z

 

inrush FL

Z e

I I





ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

2) Compute impedances and current

3) Compute voltages

3 3

3 2 3

V IZ

V I(Z Z )



 

4) Compute motor torque

1 3 2

motor

2 2

s 1 2 1 2

q V (r s)

[(r (r s)) (x x ) ]



   

Where,

s = (100 – percent speed for which acceleration time was just

computed) /100

2 n



 

120f



5) Compute accelerating torque

acc motor load

T T T 

6) Compute time for this interval

acc

t J



 

Repeat above steps till 98.5% speed is reached.

acc 1

acc acc k

t (1) t

t (k) T (k 1) t

 

   

3 3

L L

3 M L C

2 tr

sys

S 2 3

Z p.u

P jQ

Z p.u

Z Z / /Z / /Z

Z Z

Z p.u

Z Z Z Z













 

 

 

  



ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

PROGRAM:

clc;

clear all;

KW=1678.5;

KV=2.3;

RPM=1800;

J=63.87;

FLA=526.675;

f=60;

Np=4;

q=3;

tstart(1)=.5;

V1=1.026+0.0i;

V2=1.026+0.0i;

V3=1.026+0.0i;

S3p=125;

Ssys=10;

PL3=0.0;

QL3=0.0;

QC3=0.0;

Ztr=0.0001+0.0001i;

r1=0.0029;

r2=0.022;

x1=0.226;

x2=0.226;

n=input('Enter the number of values');

for j=1:n

N(j)=input('Enter the %of speed:');

K(j)=input('Enter the K value:');

PF(j)=input('Enter the power factor%:');

LT(j)=input('Enter the load torque %:');

end

flw=(2*pi*RPM)/60

flt=(KW*1000)/flw

Ns=(120*f)/Np

Ws=(2*pi*Ns)/60

MKVA=1.732*KV*FLA

Zsy=1/(S3p/Ssys);

Zs=0+(i*Zsy)

for j=2:n

PF1(j)=PF(j)/100;

PK(j)=acos(PF1(j));

Zm(j)=(1/K(j))*(cos(PK(j))+(i*sin(PK(j))))*(Ssys/MKVA)*1000

Z3(j)=Zm(j);

Z(j)=Zs+Ztr+Z3(j);

I(j)=V1/Z(j)

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

V3(j)=I(j)*Z3(j);

V2(j)=I(j)*(Ztr+Z3(j));

S(j)=(100-N(j))/100

num(j)=q*(((real(V3(j))*KV*1000)/sqrt(3))^2)*(r2/S(j));

den(j)=Ws*((r1+(r2/S(j)))^2+(x1+x2)^2);

tmotor(j)=num(j)/den(j) ;

tload(j)=(LT(j)*flt)/100;

tacc(j)=tmotor(j)-tload(j);

delt1(j)=(J*0.1*flw)/tacc(j);

tstart(j)=tstart(j-1)+delt1(j)

Istart(j)=FLA*K(j)

end

figure(1);

plot(tstart,tmotor)

Xlabel('time');Ylabel('motor torque');

figure(2);

plot(tstart,Istart)

Xlabel('time');Ylabel('starting current');

figure(3);

plot(S,tmotor)

Xlabel('slip');Ylabel('motor torque')

OUTPUT:

1) Starting current vs. time:

0 0.5 1 1.5 2 2.5 3

0.4

0.5

0.6

0.7

0.8

0.9

1.1

1.2

1.3

TIME

STARTING CURRENT

2) Torque vs. time:

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

0 0.5 1 1.5 2 2.5 3

0.5

1.5

2.5

x 10

TIME

TORQUE

3) Torque vs. slip:

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.5

1.5

2.5

x 10

SLIP

TORQUE

RESULT:

A MATLAB program was written to analyze the study of motor starting and the response of the

induction motor starting current, torque Vs slip curves were plotted.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

EXP NO:4 DATE:

LOAD FLOW ANALYSIS OF A GIVEN POWER SYSTEM WITH STATCOM

AIM:

To calculate the compensated voltage and angle in the given system using STATCOM as

the compensator

SOFTWARE REQUIRED:

Power system module of MATLAB

THEORY:

The STATCOM (or SSC) is a shunt-connected reactive-power compensation device that is

capable of generating and /or absorbing reactive power and in which the output can be varied to

control the specific parameters of an electric power system. It is in general a solid-state switching

converter capable of generating or absorbing independently controllable real and reactive power at

its output terminals when it is fed from an energy source or energy-storage device at its input

terminals. Specifically, the STATCOM considered in this chapter is a voltage-source converter

that, from a given input of dc voltage, produces a set of 3-phase ac-output voltages, each in phase

with and coupled to the corresponding ac system voltage through a relatively small reactance

(which is provided by either an interface reactor or the leakage inductance of a coupling

transformer). The dc voltage is provided by an energy-storage capacitor. A STATCOM can

improve power-system performance in such areas as the following:

1. The dynamic voltage control in transmission and distribution systems;

2. The power-oscillation damping in power-transmission systems;

3. The transient stability;

4. The voltage flicker control; and

5. The control of not only reactive power but also (if needed) active power in the connected line,

requiring a dc energy source.

Furthermore, a STATCOM does the following:

1. It occupies a small footprint, for it replaces passive banks of circuit elements by compact

electronic converters;

2. It offers modular, factory-built equipment, thereby reducing site work and commissioning time;

and

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

3. It uses encapsulated electronic converters, thereby minimizing its environmental impact.

A STATCOM is analogous to an ideal synchronous machine, which generates a balanced

set of three sinusoidal voltages at the fundamental frequency with controllable amplitude and phase

angle. This ideal machine has no inertia, is practically instantaneous, does not significantly alter the

existing system impedance, and can internally generate reactive (both capacitive and inductive)

power.

The Tennessee Valley Authority (TVA) installed the first 100-MVA STATCOM in 1995 at its

Sullivan substation. The application of this STATCOM is expected to reduce the TVA’s need for

load tap changers, thereby achieving savings by minimizing the potential for transformer failure.

This STATCOM aids in resolving the off-peak dilemma of over voltages in the Sullivan substation

area while avoiding the more labor- and space-intensive installation of an additional transformer

bank. Also, this STATCOM provides instantaneous control and therefore increased capacity of

transmission voltage, providing the TVA with greater flexibility in bulk-power transactions, and it

also increases the system reliability by damping grids of major oscillations in this grid.

EXERCISE:

Rs=0.01; Xs=0.1;Rp=200;K+=0.9

BUS DATA OF 3 BUS SYSTEM:

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Bus

no.

Bus

code

p.u.

angle

load

gen

MVAR

256.6

110.2

138.6

45.2

LINE DATA:

Bus

R pu

X pu

B pu

From

0.02

0.04

0.05

0.01

0.03

0.0125

0.025

0.06

PROGRAM:

clc;

clear all;

n=3;

pd=[0 2.562 1.102];

qd=[0 1.386 0.452];

qg=[0 0 0];

pg=[0 0 0];

vs=[1.05 1 1];

theta=[0 0 0];

con=0.1;

yb=[20-50j -10+20j -10+30j;

-10+20j 26-52j -16+32j;

-10+30j -16+32j 26-62j];

zs=0.01+0.1j;

beta=angle(zs);

rp=200;

k=0.9;

m=1;

cont=0.1;

vdc=1;

alpha=0;

b=imag(yb);

g=real(yb);

an=angle(yb);

my=abs(yb);

iter=1;

while(cont>0.01 && iter<4)

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

iter

vc=(k*k)*(m)*(vdc);

pg(3)=((vc*vs(3)*cos(theta(3)-alpha+beta))-(vs(3)*vs(3)*cos(beta)))/abs(zs);

qg(3)=((vc*vs(3)*sin(theta(3)-alpha+beta))-(vs(3)*vs(3)*sin(beta)))/abs(zs);

pac=((vc^2*cos(beta))-(vs(3)*vc*cos(beta+alpha-theta(3))))/abs(zs);

p=pg-pd;

q=qg-qd;

for o=1:n

pp(o)=0;

qq(o)=0;

for l=1:n

pe(o)=vs(o)*vs(1)*my(o,1)*cos(an(o,1)-theta(o)+theta(1))+pp(o);

pp(o)=pe(o);

qe(o)=-vs(o)*vs(1)*my(o,1)*sin(an(o,1)-theta(o)+theta(1))+qq(o);

qq(o)=qe(o);

end

pp;

qq;

pchang(1:2)=p(2:3)-pp(2:3);

qchang(1:2)=q(2:3)-qq(2:3);

pdc=(vdc^2)/rp;

pext=pac-pdc;

del=[0 0 0 0 0 ];

del=[pchang qchang pext];

%calculation of jacobian

for k=2:n

for l=1:n

if k~=1

H(k,l)=vs(k)*vs(l)*my(k,l)*sin(an(k,l)+theta(l)-theta(k));

N(k,l)=vs(k)*vs(l)*my(k,l)*cos(an(k,l)+theta(l)-theta(k));

J(k,l)=-vs(k)*vs(l)*my(k,l)*cos(an(k,l)+theta(l)-theta(k));

L(k,l)=-vs(k)*vs(l)*my(k,l)*sin(an(k,l)+theta(l)-theta(k));

else

H(k,l)=-qq(k)-vs(k)*vs(k)*b(k,k);

N(k,l)=pp(k)+vs(k)*vs(k)*g(k,k);

J(k,l)=pp(k)-vs(k)*vs(k)*g(k,k);

L(k,l)=qq(k)-vs(k)*vs(k)*b(k,k);

end

H11(1:2,1:2)=H(2:3,2:3);

N12(1:2,1:2)=N(2:3,2:3);

J21(1:2,1:2)=J(2:3,2:3);

L22(1:2,1:2)=L(2:3,2:3);

jac=zeros(5,5);

jac=[H11 N12;J21 L22];

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

jac(1,4)=0;

jac(2,2)=(vs(3)*vc*sin(theta(3)-alpha+beta)/abs(zs))-(qq(k)-vs(k)*vs(k)*b(k,k));

jac(2,4)=-(k*vdc*cos(theta(3)-alpha+beta))/abs(zs);

jac(2,5)=-(k*m*vdc*sin(theta(3)-alpha+beta))/abs(zs);

jac(3,4)=0;

jac(4,2)=-((vs(3)*vc*cos(theta(3)-alpha+beta))/abs(zs))-(pp(k)-vs(k)*vs(k)*g(k,k));

jac(4,4)=(k*vdc*vs(3)*sin(theta(3)-alpha+beta))/abs(zs);

jac(4,5)=-(k*vdc*vs(3)*cos(theta(3)-alpha+beta))/abs(zs);

jac(5,2)=-(k*vdc*m*vs(3)*sin(alpha-theta(3)+beta))/abs(zs);

jac(5,4)=(k*m*vs(3)*vdc*sin(alpha-theta(3)+beta))/abs(zs);

jac(5,5)=-((vdc*k*vs(3)*cos(alpha-theta(3)+beta))-(2*k*k*m*vdc^2*cos(beta)))/abs(zs);

jac;

delta=(jac)\del';

dtheta(2:3)=delta(1:2);

theta=theta+dtheta

dv=[0 0 0];

dv(2:2)=delta(3:3);

vs=vs+dv

con=max(abs(dv));

iter=iter+1;

m=m+delta(4);

alpha=alpha+delta(5);

end

OUTPUT:

iter = 1

theta = 0 -0.0262 0.0033

vs = 1.0500 0.9778 1.0000

iter = 2

theta = 0 -0.1781 -0.2471

vs = 1.0500 0.9770 1.0000

iter = 3

theta = 0 -0.5447 -0.8483

vs = 1.0500 0.9305 1.0000

RESULT:

Thus the compensated voltage and angle in the given system is calculated by using

STATCOM as the compensator

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

EXP NO:5 DATE:

TRANSIENT ANALYSIS OF SINGLE MACHINE INFINITE BUS (SMIB) SYSTEM

WITH STATCOM

AIM:

To analyse the transient performance of Single Machine Infinite Bus (SMIB) system with

STATCOM using MATLAB.

THEORY:

A STATCOM is a voltage- sourced converter (VSC) –based shunt FACTS device and is

capable of injecting controllable reactive current into the system. Consider that a STATCOM is

placed at bus m in the SMIB system as shown in Fig.(1).The equivalent circuit of the system is

shown in Fig.(2) where the STATCOM is represented by a shunt reactive current source I

Fig 1 Schematic diagram of SMIB system with STATCOM

Fig 2 Equivalent Circuit of SMIB system with STATCOM

STATCOM

Infinite

bus

BUS

E



V0

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

STATCOM can be represented by a shunt reactive current source I

δ π/2)

s s

I I e





(1)

Here δ

is the angle of voltage at bus m and is given by

1 2

E'X sin

δ tan

VX E'X cos



 



 



 

(2)

2 m 1 m 1 2

m s

1 2 1 2

E'X cos(

δ δ ) VX cosδ X X

V I

X X X X

 

 

 

(3)

Where, δ is the angle of the machine, X1 represents the equivalent reactance between the machine

internal bus and the intermediate bus m, X2 represents the equivalent reactance between bus m and

the infinite bus, E’ is the machine internal voltage and V is the infinite bus voltage.

The above equations Eq.(2) and Eq.(3) indicates that the angle δ

is independent of I

but the bus

voltage V

depends upon I

. The electrical power P

of the machine can be written as

e m

E'V

P sin(

δ δ )

 

(4)

Substituting the value of V

and δ

in Eq.(4)

2 m 1 m 1 2

e m s m

1 1 2 1 1 2

E'X cos(

δ δ ) VX cosδ X X

E' E'

P sin(

δ δ ) I sin(δ δ )

X X X X X X

   

 

   

   

 

   

(5)

Applying some basic circuit equations P

written as

max

sinδ+f

(δ)I

(6)

Where,

max

1 2

E'V

X X





(7)

1 m

1 2

E'X

f (

δ) sin(δ δ )

X X

 



(8)

Note that f

(δ) is positive when δ oscillates between zero and π Eq.(6) suggests that P

can

be modulated by controlling the STATCOM current I

.it may be mentioned here that I

in eq.(6) is

positive (negative) for capacitive (inductive) operation of the STATCOM.

The speed of the machine ω is an appropriate control signal that can be used to

enhancement of the power system damping. With the above control I

can be expressed as

ω , I

min

≤ I

max

(9)

Here, K1 is a positive gain and it depends upon the maximum current rating (I

max

) of the

STATCOM. From the mathematical model (Eqns.6, 7, 8 & 9).The simulation block diagram of the

SMIB system with STATCOM is shown in the Fig.(3).

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Fig 3 Simulation block diagram of SMIB system with STATCOM Controller

Using Eq.(6) and Eq.(9) -E can be written as

-E (δ, ω) = [D+K

(δ)] ω

(10)

Here –E is considered as the rate of dissipation of transient energy. The first term within the

square bracket of Eq.(10) is the natural damping coefficient D and the second term can be

considered as additional damping coefficient (D

STAT

) provided by the STATCOM.

STAT 1 1 1 m

1 2

E'X

D K f (

δ) K sin(δ δ )

X X

  



(11)

The above equations indicates that the value of D

STAT

depends on the reactances (X

)

,and hence the location of STATCOM. When the STATCOM is placed near the infinite bus

→0), D

STAT

of Eq.(11) approaches to zero..On the other hand, when X

tends to zero, δ

Eq.(2) becomes almost the same as δ, and hence D

STAT

is also approaches to zero. For a given δ, it

can be shown that the maximum value of D

STAT

can be obtained when the reactance ratio

=(X

) becomes the same as the voltage ratio a

= (E’/V).For such case, δ

of Eq.(2) becomes

δ/2, and thus the maximum damping coefficient provided by the STATCOM can be expressed as:

max

STAT 1

D K sin( )

a 1 2





(12)

Here, a=a

Data for the SMIB system:

Generator: X`=0.3 pu, f=60 Hz, D=0, H=5s (M=H/f).

Transformer: X=0.1 pu.

Transmission lines: X=0.4 pu of each line.

The generator initially delivers a power of 1.0 pu at a terminal voltage of 1.05 pu and the

infinite bus voltage of 1.0 pu. The generator internal voltage E` for the above operating condition is

found as 1.235640.35

pu.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Simulation Diagram of SMIB with STATCOM

Continuous

powergui

1/377

Transfer Fcn

Step

Scope

Product1

Product

Integrator

-k

Gain3

-k

Gain2

-k

Gain1

-k

Gain

f(u)

Fcn1

f(u)

Fcn

OUTPUT:

ROTOR ANGLE RESPONSE WITHOUT STATCOM:

0 1 2 3 4 5 6 7 8 9 10

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

0.18

TIME (SEC)

ROTOR ANGLE (DEGREE)

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

ROTOR ANGLE RESPONSE WITH STATCOM:

0 1 2 3 4 5 6 7 8 9 10

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

TIME (SEC)

ROTOR ANGLE (DEGREE)

INFERENCE:

From the output response we can understand that with the inclusion of STATCOM the

SMIB system regains its rotor angle stability whereas without STATCOM the oscillations

continued and rotor angle stability could not be regained.

RESULT:

The transient performance of the Single Machine Infinite Bus (SMIB) system with

STATCOM was analysed using MATLAB.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

EXNO:6 DATE :

AVAILABLE TRANSFER CAPABILITY CALCULATION USING AN EXISTING LOAD

FLOW PROGRAM (FAST DECOUPLED LOAD FLOW METHOD)

AIM:

To calculate the value of Available Transfer Capability using Fast decoupled load flow

method.

SOFTWARE REQUIRED:

Power system module of MATLAB.

THEORY:

All over the world, power systems are being deregulated, restructured and privatized with an

objective to introduce competition and to improve the efficiency and economy of operation. Single

utility is divided into different independent organizations such as Gencos, Transcos and Discos.

Gencos and Discos are given open access to transmission grid. An Independent System

Operator (ISO) regulates and maintain the grid sale of power (MW) between these Gencos and

Discos is encouraged and these transactions are called bilateral transactions.

The market participants, gencos and discos, need to know the “Available Transfer Capacity

(ATC)” between various source nodes (Genco buses) , and sink nodes (Disco buses) of the gird

tomorrow in order to finalize these bilateral transactions. ATC between a source node ‘k’ and a

sink node ‘m’ is defined as the difference between the “Total Transfer Capacity (TTC)” of MW

power between nodes k and m and the base case MW flow (BCMW) between k and m.

ATCkm = TTCkm – BCMWkm

The TTCkm is the maximum MW power that can be transferred in the system between the

source node k and the sink node m without violating the line flow and bus voltage operating limits.

ATCkm can be determined by conducting repeated Load Flow analysis on the system

starting with the base case load and increasing the generation at the kth bus and demand at the mth

bus by certain percentage until any of the line flow or bus voltage constraints is just violated. The

increased generation/load over the base case is the ATCkm.

EXERCISE:

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Using a text editor create an input data file in the sequence given below for load flow solution of

the 6-bus system. Run the program and print the output file. Check the results obtained using the

available software.

(i)Consider the optimal operating state for the base case loading of the 6 bus system.

Determine the ATC between the “source bus” 1 and “sink bus”5 for base case operating

state. Limit on bus voltage magnitude:0.9<V<1.05 p.u.

Bus Data:

Bus

NO.

BUS

Code

Voltage

Magnitude

p.u.

Angle

degrees

Load

generation

MVAR

min

MAX

1.05

-50

100

1.05

-25

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Transmission Line Data:

Line

No.

Send bus

No.

Received

Bus

No.

Resistance

p.u.

Reactanc

p.u.

Half line

Charging

Susceptance p.u.

Rating

MVA

0.123

0.518

0.08

0.37

0.087

0.407

0.282

0.64

0.723

1.05

0.300

0.133

Transformer Data:

Transformer ID no.

Send bus no.

Receive bus no.

Tap ratio

0.956

0.981

Shunt element data:

Shunt id no.

Bus id no.

Rated capacity MVAR

5.5

PROGRAM:

clear all;

clc;

r1=input('enter the reactance b/w 1 & 2');

r2=input('enter the reactance b/w 2 & 3');

r3=input('enter the reactance b/w 1 & 3');

temp=[(r1+r2) r1 r3;r1 (r1+r2) r2;r3 r2 (r3+r2)];

mw1=input('enter max mw limit b/w 1 and 2');

mw2=input('enter max mw limit b/w 2 and 3');

mw3=input('enter max mw limit b/w 1 and 3');

bo=[((1/r1)+(1/r2)) -(1/r2);-(1/r2) (1/r3)+(1/r2)]

xo=inv(bo)

disp('====ptdf cal b/w 1&3====')

ptdf1=xo(1,2)/r1

ptdf2=xo(2,2)/r3

ptdf3=(-xo(1,2)+xo(2,2))/r2

disp('====ptdf cal b/w 1&2====')

ptdf4=(-xo(1,1)+xo(1,2))/r1

ptdf5=(-xo(2,1)+xo(2,2))/r3

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

ptdf6=(xo(1,1)-xo(2,1)-xo(1,2)+xo(2,2))/r2

disp('====power flow due to transactions===')

a=[ptdf1 ptdf4;ptdf2 ptdf5;ptdf3 ptdf6]

b=[mw2;mw3]

p=[a]*[b]

disp('power flow due to transactions b/w 1&3 and 2&3:');

disp(p);

p1=p(1,1);

p2=p(2,1);

p3=p(3,1);

disp('===atc cal b/w 1&3===')

pmax12=(mw1-p1)/ptdf1

pmax13=-(mw2-p2)/ptdf2

pmax23=(mw3-p3)/ptdf3

disp('===atc cal b/w 2&3===')

pmax12=(mw1-p1)/ptdf4

pmax13=-(mw2-p2)/ptdf5

pmax23=(mw3-p3)/ptdf6

OUTPUT

enter the reactance b/w 1 & 20.1

enter the reactance b/w 2 & 30.066

enter the reactance b/w 1 & 30.05

enter max mw limit b/w 1 and 2600

enter max mw limit b/w 2 and 3200

enter max mw limit b/w 1 and 3600

bo =25.1515 -15.1515

-15.1515 35.1515

xo = 0.0537 0.0231

0.0231 0.0384

====ptdf cal b/w 1&3====

ptdf1 = 0.2315

ptdf2 =0.7685

ptdf3 =0.2315

====ptdf cal b/w 1&2====

ptdf4 =-0.3056

ptdf5 = 0.3056

ptdf6 =0.6944

====power flow due to transactions===

a =0.2315 -0.3056

0.7685 0.3056

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

0.2315 0.6944

b = 200

600

p =-137.0370

337.0370

462.9630

power flow due to transactions b/w 1&3 and 2&3:

-137.0370

337.0370

462.9630

===atc cal b/w 1&3===

pmax12 =3.1840e+003

pmax13 =178.3133

pmax23 = 592.0000

===atc cal b/w 2&3===

pmax12 = -2.4121e+003

pmax13 = 448.4848

pmax23 = 197.3333

OUTPUT FOR INCREMENT OF 10 MW AT SINK BUS:

Increment of steps

(MW)

Voltage magnitude at load buses

0.925

0.929

0.903

0.904

0.923

0.925

0.896

0.897

ATC = 10MW

INFERENCE:

Therefore an increment by 10MW with the base case values it has been found that the

voltage profile of buses 5 & 6 reaching below 0.9. Therefore it is a voltage limited case

(ii)Consider the optimal operating state for the base case loading of the 6 bus system.

Determine the ATC between the “source bus” 1 and “sink bus”3 for base case operating

state. Limit on bus voltage magnitude:0.9<V<1.05 p.u

OUTPUT FOR INCREMENT OF 15 MW AT SINK BUS:

Increment of steps

(MW)

Voltage magnitude tn load buses

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

0.919

0.905

0.907

0.906

0.912

0.918

0.905

0.902

0.904

0.910

0.903

0.898

ATC = 15 MW

INFERENCE:

Therefore an increment by 15 MW with the base case values it has been found that the

voltage profile of the bus 6 reaching below 0.9. Therefore it is a voltage limited case.

RESULT:

Thus the value of ATC (Available Transfer Capability) between buses 1 & 5 and buses 1 &

3 are calculated using Fast Decoupled load flow method.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

EXPNO:7 DATE:

STUDY OF DFIG BASED WIND ENERGY CONVERSATION SYSTEM

AIM:

To study of doubly fed induction generator based wind energy conversation system

THEORY:

FUNDAMENTALS OF WIND TURBINES.

The power extracted from the wind can be calculated by the given formula:

= extracted power from the wind,

ρ = air density, (approximately 1.225 kg/m

at 20

₀

C at sea level)

R = blade radius (in m), (it varies between 40-60 m)

= wind velocity (m/s) (velocity can be controlled between 3 to 30 m/s)

= the power coefficient which is a function of both tip speed ratio (λ), and blade pitch angle,

(β) (Degrees)

Power coefficient (C

) is defined as the ratio of the output power produced to the power available

in the wind.

Betz Limit:

No wind turbine could convert more than 59.3% of the kinetic energy of the wind into

Mechanical energy turning a rotor. This is known as the Betz Limit, and is the theoretical

Maximum coefficient of power for any wind turbine. The maximum value of C

according to

Betz limit is 59.3%. For good turbines it is in the range of 35-45%.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Figure 2.6 Power Speed Characteristics of Wind Turbine

Torque speed characteristics

Studying the torque versus rotational speed characteristics of any prime mover is very important

for properly matching the load and ensuring stable operation of the electrical generator. The

typical torque speed characteristics of the two – blade propeller- type wind turbine, the Darrieus

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

rotor, and the Savonius rotor are shown in figure. The profiles of the Torque-speed curves shown

in the figure follow from the power curves, since torque and power are related as follows

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Wind Turbine Control Systems

Pitch Angle Control:

The system changes the pitch angle of the blades according to the variation of wind speed. As discussed earlier, with

pitch control, it is possible to achieve a high efficiency by continuously aligning the blade in the direction of the

relative wind.

On a pitch controlled machine, as the wind speed exceeds its rated speed, the blades are gradually turned about the

longitudinal axis and out of the wind to increase the pitch angle. This reduces the aerodynamic efficiency of the

rotor, and the rotor output power decreases. When the wind speed exceeds the safe limit for the system, the pitch

angle is so changed that the power output reduces to zero and the machine shifts to the

„

stall

‟

mode. After the gust

passes, the pitch angle is reset to the normal position and the turbine is restarted. At normal wind speeds, the blade

pitch angle should ideally settle to a value at which the output power equals the rated power. The input variable to

the pitch controller is the error signal arising from the difference between the output electrical power and the

reference power. The pitch controller operates the blade actuator to alter the pitch angle. During operation below the

rated speed, the control system endeavours to the pitch the blade at an angle that maximises the rotor efficiency. The

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

generator must be able to absorb the mechanical power output and deliver to the load. Hence, the generator output

power needs to be simultaneously adjusted.

StallControl

Passive stall control:

Generally, stall control to limit the power output at high winds is applied to constant-pitch turbines driving

induction generators connected to the network. The rotor speed is fixed by the network, allowing only 1-4%

variation. As the wind speed increases, the angle of attack also increases for a blade running at a near constant speed.

Beyond a particular angle of attack, the lift force decreases, causing the rotor efficiency to drop. This lift force can

be further reduced to restrict the power output at high winds by properly shaping the rotor blade profile to create

turbulence on the rotor blade side not facing the wind.

Active stall control:

In this method of control, at high wind speeds, the blade is rotated by a few degrees in the direction opposite to that

in a pitch controlled machine. This increases the angle of attack, which can be controlled to keep the output power

at its rated value at all high wind speeds below the furling speed. A passive controlled machine shows a drop in

power at high winds. The action of active stall control is sometimes called deep stall. Owing to economic reasons,

active pitch control is generally used only with high- capacity

machines.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Figure 3.2 – Power versus wind speed characteristics of variable speed wind turbines

In the intermediate speed-range, the control strategy depends on the type of electrical power generating system used,

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

and can be divided into two basic categories:

a) Constant speed generation scheme, and b)

Variable-speed generation scheme.

If the electrical system involves a grid-connected synchronous generator, the constant generation scheme is

necessary. In the case of grid-connected squirrel cage induction generators, the allowable range of speed

variation is very small, requiring an almost constant rotational speed.

But the constant-speed generation systems cannot maximise the power extraction from wind. Power coefficient

reaches a maximum specific value of TSR for every type of wind turbine. Hence for the extraction of maximum

power from wind, the turbine should operate at a constant TSR, which means the rotational speed should be

proportional to the wind speed. So maximum power extraction requires a variable-speed generation system with the

speed control for keeping a constant TSR.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

This scheme has a few disadvantages. First, the wind speed measured in the neighbourhood of a wind turbine

(or a wind farm) is not reliable indicator of V because of the shadowing effects. Also it is difficult to

determine the value of TSR for maximum C

. This value changes during the lifetime of a wind turbine due to the

changes in the reference setting.

A second control scheme is devised to continuously track the maximum power point (MPP) using the property

that the C

versus TSR curve has a single smooth maximum point. This means that if operate at the maximum

power point, small fluctuations in the rotational speed do not significantly change the power output. To

implement this scheme, the speed is varied in small steps, the power output is measured and, and ΔP/Δω is

evaluated. If this ratio is positive, more mechanical power can be obtained by increasing the speed.

Hence the electrical power output is decreased temporarily by the power electronic control so that the speed

increases. This increases the mechanical power, and can be obtained by increasing the speed. Hence the

electrical power output is decreased temporarily by power electronic

control so that the speed increases. This increases the mechanical power, and the electrical power, and the

electrical power output is decreased temporarily by the power electronic control so that the speed

increases. This increases the mechanical power, and the electrical power is again raised to a higher value. The

process continues until the optimum speed is reached, when the mechanical power becomes intensive to speed

fluctuations. When the wind speed changes, this mechanism readjusts the speed at the optimum value.

While controlling the rotational speed, it should be remembered that a large difference between

mechanical power and electrical power results in a large torque and, hence, a large stress on the rotor

components. It is necessary to limit the acceleration and deceleration rates to values dictated by the structural

strength of mechanical parts.

DOUBLY FED INDUCTION GENERATOR

1. In a doubly fed induction machine, two windings participate in energy conversion process.

They can work at double the synchronous speed for constant torque, similar to synchronous machine

but in synchronous machine only one winding participate in energy conversion DFIM (doubly fed

induction machine) is to operate in narrow speed ranges.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

2. CONSTRUCTION

1. Wound Rotor DFIM.

2. Brushless wound rotor:

a. Brushless DF Induction electric machine.

b. Brushless wound rotor DF electric machine.

Wound rotor DFIM uses the two windings of same power rating. One is winding on stator

and the other on rotor. Stator supply is Normal 3 phase supply. Rotor supply is from power

frequency converter. Slip ring assembly used to transfer Power to rotor winding. In a

brushless DFIM two windings are adjacent to each the other on stator. Windings are excited

separately. Brushless wound rotor DFIM is similar to wound rotor DFIM but slip ring

assembly is not used. It has a large efficiency and less cost but instability is more.

WORKING:

Field can be from rotor or stator or from both. Both active power (for torque) and reactive

power (for flux) have to be fed to rotor. Multi-phase supply with frequency f is given to

stator. Control Frequency converter converts power from supply frequency to slip frequency.

ADVANTAGES:

 Theoretically system cost is half of other machines with same rating.

 Higher efficiency can be achieved due to less loss.

 Rotor core is effectively utilized hence power density is large.

 Active and reactive power to grid can be controlled using electronic converters

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

 DFIG can work in variable speed range around synchronous speed

Wound rotor DFIM found commercial success in very large applications with limited speed

range. For a low cost, highly efficient and reliable electronic controlled DFIM is kept

under study

Figure 4.4 – DFIG Connected to the

Grid

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

control so that the speed increases. This increases the mechanical power, and the electrical power, and the electrical power

output is decreased temporarily by the power electronic control so that the speed increases. This increases the

mechanical power, and the electrical power is again raised to a higher value. The process continues until the optimum speed

is reached, when the mechanical power becomes intensive to speed fluctuations. When the wind speed changes, this

mechanism readjusts the speed at the optimum value.

While controlling the rotational speed, it should be remembered that a large difference between mechanical power

and electrical power results in a large torque and, hence, a large stress on the rotor components. It is necessary to limit the

acceleration and deceleration rates to values dictated by the structural strength of mechanical parts.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

WIND FARM ‐ DFIG DETAILED MODEL

SIMULATION:

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

OUTPUT:

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

EXPNO:8 DATE:

STUDY OF VARIABLE SPEED WIND ENERGY CONVERSION SYSTEM-

PMSG

AIM:

To study of variable speed wind energy conversion system using Permenant

magnet synchrouns generator

THEORY:

Sustainability is the main aspect that forces the renewable energy sources to be implemented for

electric energy generation instead of fossil ones. Wind energy is quite attractive among other sources

because of its commercial potential [72 TW] that is five times higher than world energy demand in all

forms. However, the installed capacity in 2009 was only 159GW. Large turbines play a main role on the

market, but there is also demand for small turbines in the power range up to 11 kW as the power source

for micro generators. Micro generator is an electrical energy source that includes all interface units and

operates in parallel with the distribution network.

Current rating of such devices is limited up to 16 A per phase. Some energy sources can be

connected directly to the distribution network, but in the case of DC power sources or variable speed

wind turbine (VSWT) systems it is necessary to use a power converter that interfaces the source and the

grid.VSWT based micro generators consist of a wind turbine, a generator and an inverter. Wind turbines

capture wind energy and convert it to rotational mechanical energy. Variable speed operation of the

wind turbine allows extraction of higher energy from wind than constant speed systems. The generator

converts mechanical energy into electricity. Different types of generators can be used in wind energy

conversion systems (WECS), but permanent magnet synchronous generators (PMSG) play a main role

on the market. The main advantage of PMSG is the possibility of multipole design that offers slow speed

operation and the possibility of gearless WECS construction. Another advantage is maintenance free

operation since there are no brushes. The main drawback of PMSG is the dependence of its output

voltage on the rotation speed. The difference between the minimum and the maximum voltage can reach

four times in VSWT applications.

This drawback can be easily overcome with the help of an appropriate interfacing converter.The

interfacing converter rectifies the input AC with variable voltage and frequency, adjusts voltage levels

and inverts DC voltage into AC with grid voltage and frequency. Additionally, it should have maximum

power point tracking (MPPT) functionality to extract more power from wind.The new topology of the

interfacing converter with the HF isolation transformer for PMSG based VSWT system is presented in

this paper. The topology presented has good voltage regulation capabilities at a relatively simple power

circuit.

DIFFERENT TOPOLOGIES INTERFACING CONVERTER FOR WIND TURBINE.

Basically they can be divided into two groups: topologies without galvanic isolation (Fig. 1a) and

those with isolation. Line frequency (LF) transformers (Fig. 1b) were widely used for galvanic isolation

in last decades.Main drawbacks of LF transformer are high weight and high price. For these reasons

topologies with HF isolation (Fig. 1c) have became popular especially for photovoltaic applications and

wind power applications.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Fig 1:Block diagram of interfacing converters

CHALLENGES OF PMSG BASED VSWT

This section introduces the concept of wind energy,properties of wind energy, emphasizing

wind energy extraction by means of PMSG based VSWT. Operation modes of VSWT with fixed blades

are analyzed and generator characteristics are given.

ENERGY FROM THE WIND

Wind is simple air in motion. It is caused by the uneven heating of the earth’s surface by the sun.

Since the earth’s surface is made of very different types of land and water, it absorbs the sun’s heat at

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

different rates. During the day, the air above the land heats up more quickly than the air over water. The

warm air over the land expands and rises, and the heavier, cooler air rushes in to take its place, creating

winds. At night, the winds are reversed because the air cools more rapidly over land than over water. In

the same way, the large atmospheric winds that circle the earth are created because the land near the

earth's equator is heated more by the sun than the land near the North and South Poles. Today, wind

energy is mainly used to generate electricity. Wind is called a renewable energy source because the wind

will blow as long as the sun shines.

THE HISTORY OF WIND

Since ancient times, people have harnessed the winds energy. Over 5,000 years ago, the ancient

Egyptians used wind to sail ships on the Nile River. Later, people built windmills to grind wheat and

other grains. The earliest known windmills were in Persia (Iran). These early windmills looked like large

paddle wheels. Centuries later, the people of Holland improved the basic design of the windmill. They

gave it propeller-type blades, still made with sails. Holland is famous for its windmills.American

colonists used windmills to grind wheat and corn, to pump water, and to cut wood at sawmills. As late as

the 1920s, Americans used small windmills to generate electricity in rural areas without electric service.

When power lines began to transport electricity to rural areas in the 1930s, local windmills were used

less and less, though they can still be seen on some Western ranches. The oil shortages of the 1970s

changed the energy picture for the country and the world. It created an interest in alternative energy

sources, paving the way for the re-entry of the windmill to generate electricity. In the early 1980s wind

energy really took off in California, partly because of state policies that encouraged renewable energy

sources. Support for wind development has since spread to other states, but California still produces

more than twice as much wind energy as any other state. The first offshore wind park in the United

States is planned for an area off the coast of Cape Cod, Massachusetts.

HOW THE WIND MACHINES WORK

Like old fashioned windmills, today’s wind machines use blades to collect the wind’s kinetic

energy. Windmills work because they slow down the speed of the wind. The wind flows over the airfoil

shaped blades causing lift, like the effect on airplane wings, causing them to turn. The blades are

connected to a drive shaft that turns an electric generator to produce electricity. With the new wind

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

machines, there is still the problem of what to do when the wind isn’t blowing. At those times, other

types of power plants must be used to make electricity

TYPES OF WIND MACHINES

There are two types of wind machines (turbines) used today based on the direction of the rotating

shaft (axis): horizontal–axis wind machines and vertical-axis wind machines. The size of wind machines

varies widely. Small turbines used to power a single home or business may have a capacity of less than

100 kilowatts. Some large commercial sized turbines may have a capacity of 5 million watts, or 5

megawatts. Larger turbines are often grouped together into wind farms that provide power to the

electrical grid.

HORIZONTAL AXIS WIND MACHINE

Most wind machines being used today are the horizontal-axis type. Horizontal-axis wind

machines have blades like airplane propellers. A typical horizontal wind machine stands as tall as a 20-

story building and has three blades that span 200 feet across. The largest wind machines in the world

have blades longer than a football field! Wind machines stand tall and wide to capture more wind.

VERTICAL AXIS WIND MACHINE

Vertical–axis wind machines have blades that go from top to bottom and the most common type

(Darrieus wind turbine) looks like a giant two-bladed egg beaters. The type of vertical wind machine

typically stands 100 feet tall and 50 feet wide. Vertical-axis wind machines make up only a very small

percent of the wind machines used today.

The Wind Amplified Rotor Platform (WARP) is a different kind of wind system that is designed

to be more efficient and use less land than wind machines in use today. The WARP does not use large

blades; instead, it looks like a stack of wheel rims. Each module has a pair of small, high capacity

turbines mounted to both of its concave wind amplifier module channel surfaces. The concave surfaces

channel wind toward the turbines, amplifying wind speeds by 50 percent or more. Eneco, the company

that designed WARP, plans to market the technology to power offshore oil platforms and wireless

telecommunications systems.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

WIND POWER PLANTS.

Wind power plants, or wind farms as they are sometimes called, are clusters of wind machines

used to produce electricity. A wind farm usually has dozens of wind machines scattered over a large

area. The world's largest wind farm, the Horse Hollow Wind Energy Center in Texas, has 421 wind

turbines that generate enough electricity to power 220,000 homes per year. Unlike power plants, many

wind plants are not owned by public utility companies. Instead they are owned and operated by business

people who sell the electricity produced on the wind farm to electric utilities. These private companies

are known as Independent Power Producers. Operating a wind power plant is not as simple as just

building a windmill in a windy place. Wind plant owners must carefully plan where to locate their

machines. One important thing to consider is how fast and how much the wind blows. As a rule, wind

speed increases with altitude and over open areas with no windbreaks. Good sites for wind plants are the

tops of smooth, rounded hills, open plains or shorelines, and mountain gaps that produce wind

funneling. Wind speed varies throughout the country. It also varies from season to season. In Tehachapi,

California, the wind blows more from April through October than it does in the winter. This is because

of the extreme heating of the Mojave Desert during the summer months. The hot air over the desert

rises, and the cooler, denser air above the Pacific Ocean rushes through the Tehachapi mountain pass to

take its place. In a state like Montana, on the other hand, the wind blows more during the winter.

Fortunately, these seasonal variations are a good match for the electricity demands of the regions. In

California, people use more electricity during the summer for air conditioners. In Montana, people use

more electricity during the winter months for heating.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

COMPONENTS OF THE WIND TURBINE

Fig 2:Wind turbine components

Anemometer:

Measures the wind speed and transmits wind speed data to the controller.

Blades:

Most turbines have either two or three blades. Wind blowing over the blades causes the blades to

"lift" and rotate.

Brake:

A disc brake, which can be applied mechanically, electrically, or hydraulically to stop the rotor in

emergencies.

Controller:

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

The controller starts up the machine at wind speeds of about 8 to 16 miles per hour (mph) and

shuts off the machine at about 55 mph. Turbines do not operate at wind speeds above about 55

mph because they might be damaged by the high winds.

Gear box:

Gears connect the low-speed shaft to the high-speed shaft and increase the rotational speeds from

about 30 to 60 rotations per minute (rpm) to about 1000 to 1800 rpm, the rotational speed

required by most generators to produce electricity. The gear box is a costly (and heavy) part of the

wind turbine and engineers are exploring "direct-drive" generators that operate at lower rotational

speeds and don't need gear boxes.

Generator:

Usually an off-the-shelf induction generator that produces 60-cycle AC electricity.

High-speed shaft:

Drives the generator.

Low-speed shaft:

The rotor turns the low-speed shaft at about 30 to 60 rotations per minute.

Nacelle:

The nacelle sits atop the tower and contains the gear box, low- and high-speed shafts, generator,

controller, and brake. Some nacelles are large enough for a helicopter to land on.

Pitch:

Blades are turned, or pitched, out of the wind to control the rotor speed and keep the rotor from

turning in winds that are too high or too low to produce electricity.

Rotor:

The blades and the hub together are called the rotor.

Tower:

Towers are made from tubular steel (shown here), concrete, or steel lattice. Because wind speed

increases with height, taller towers enable turbines to capture more energy and generate more

electricity.

Wind direction:

This is an "upwind" turbine, so-called because it operates facing into the wind. Other turbines are

designed to run "downwind," facing away from the wind.

Wind vane:

Measures wind direction and communicates with the yaw drive to orient the turbine properly with

respect to the wind.

Yaw drive:

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Upwind turbines face into the wind; the yaw drive is used to keep the rotor facing into the wind as

the wind direction changes. Downwind turbines don't require a yaw drive, the wind blows the

rotor downwind.

Yaw motor:

Powers the yaw drive.

WIND TURBINE CHARACTERACTICS

Equation (1) gives the total power available in the wind,where A is the rotor area, ρ is the air

density and v is the wind velocity.

WIND

= 0.5Aρv

…………… (1)

Only a part of the total wind energy can be extracted. The available energy part in wind is

described by the power coefficient C

. The theoretical maximum value of this coefficient is 0.59 and it is

called the Betz limit.

turbine

=0.5C

………… (2)

The practical values of Cp lie between 0.4 and 0.5 for industrial wind turbines.This power

coefficient is a function of the tip-speed ratio λ. An example of this function is shown in Fig. 2. The tip-

speed ratio shows the relation between the circumferential velocity of the blade tips and the wind

velocity:

………………..(3)

where r is the rotor radius and Ω is the angular rotor speed.

Fig. 3. Power coefficient C

vs. tip-speed ratio.

Rotors are usually designed so that power coefficient C

has the maximum values at the-speed

ratio in the range from 4 to 8.Since the coefficient C

is the function of the tip-speed ratio the power

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

extracted by the wind turbine depends on the wind velocity and the rotational speed. Power curves at

different wind velocities for turbines with fixed blade position shown in Fig. 3.

Fig. 4 indicates that the maximal power can be captured from wind turbines only if they are of a

variable speed type. This figure illustrates also another feature of variable speed turbines: generator’s

speed is four times lower at the cut-in wind speed than at the rated velocity. The wind velocity

determines the rotational speed of the wind turbine and the generator.

Since it as direct impact on power converter operation modes, an example of wind velocity

distribution at 10 meter height is shown in Fig. 5, but the corresponding energy yield in Fig. 6. Three

distinct operating modes of the variable speed wind turbine generator can be emphasized: slow speed,

rated speed and high speed. Slow speed occurs when the wind velocity lies in the range from 3m/s till

7m/s, rated speed - 7...8m/s and high speed mode is at higher velocities. This division of modes is made

according to the normalized energy yield (Fig. 6). The rated speed corresponds to wind velocity with

maximum energy distributions are characteristic of Baltic coastal regions and so can be used as reference

for interface converter design. The distribution of wind velocity per wind turbine modes is presented in

Table I. It shows that the wind turbine is silent one quarter of the time and half of the time works at low

speed.

Fig. 4. VSWT power vs. rotation speed of turbine at different wind velocities.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Fig. 5. An example of wind velocity distribution.

Fig. 6. An example of normalized energy yield.

NEED OF PERMANENT MAGNET SYNCHRONOUS GENERATOR IN WIND TURBINE

GRID SYSTEM

Optimum wind energy extraction is achieved by running the wind turbine generator (WTG) in

variable-speed variable- frequency mode. The rotor speed is allowed to vary in sympathy with the wind

speed by maintaining the tip speed ratio to the value that maximizes aerodynamic efficiency. In order to

achieve this ratio, the permanent-magnet synchronous generator (PMSG) load line should be matched

very closely to the maximum power line of the wind turbine generator. In such a case, a good matching

exists between the generator and the load for the best performance of the system, as well as the maximum

utilization of the wind driven PMSG. However, the recent advancements in power electronics and control

strategies have made it possible to regulate the voltage of the PMSG in many different ways. When the

generator torque line can be controlled, the generator loading of the turbine can be made to follow the

desired locus such as the optimum shaft power locus.

PMSG MODEL

The PMSG dynamic equations are expressed in the “ reference” frame. The model of electrical dynamics

in terms of voltage and current can be given by the following equations

…………………….(4)

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

where R and L are the machine resistance and inductance per phase, and are the two-axis machine

voltages, and i

and i

are the two-axis machine currents. is the amplitude of the flux linkages

established by the permanent magnet, and

The above equations are derived assuming that the q -axis is aligned with the stator terminal

voltage phasor (i.e.v

=0, ). The expression for the electromagnetic (EM) torque in the rotor is written as

………………………..(5)

Where P is the number of poles of the PMSG, and T

is the electrical torque from the generator.

The relationship between the angular frequency of the stator voltage and the mechanical angular

velocity of the rotor may be expressed as

……………………(6)

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

PMSG BASED WIND TURBINE.

PMSG based VSWTs have three distinct operation modes: silent mode, variable speed operation

mode and constant speed mode. A turbine is silent in two cases: wind speed is below a cut-in level or

above the cut-off speed. If the speed is below its cut-in level it produces insufficient torque to move the

turbine. At the same time winds above the cut-off level may damage the turbine that must be stopped at

such conditions. A turbine usually starts to operate at 3 m/s and it should be stopped at the wind speed

above 25 m/s.Turbines operate at variable speed in the wind velocity range from cut-in to rated wind

speed. Rated wind speed differs by turbine types, but often has the value of 12 meters per second.

Constant speed mode takes palace above the rated wind speed. Turbine output power remains constant at

this mode (Fig. 7).PMSGs with 8 pole pairs are considered as a power source in this research. Its line

voltage is 140V at 375 rpm, but it can operate up to 510 rpm. This speed is considered as the maximum

power operational point for the turbine and the generator. Generator power reaches 1250W at this point,

but the output voltage is 183V.

Fig. 7. Output power of VSWT.

Cut-in speed for a turbine is 125 rpm and it can produce 20W, but the generator voltage is only

48V at this point. So this is the lowest input voltage for a converter. Generator speed and voltage

characteristics are shown in Fig. 7.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Fig. 8. Generator speed and voltage vs. wind speed.

TOPOLOGIES OF INTERFACE CONVERTERS FOR PMSG BASED VSWT

Interface converter for a PMSG based VSWT can have different topologies. Topologies with HF

isolation for VSWT application already known are studied in this section to evaluate their pros and cons

in the context of the described PMSG utilization in such systems and a new interface converter topology

with qZS DC/DC converter based HF isolation is offered.

3.1.1 TRADITIONAL TOPOLOGIES.

There are only few converter topologies with high frequency isolation for small wind applications

studied in the literature. In old technologies proposed a buck type isolated DC/DC converter (Fig. 9a).

Variable generator voltage is rectified with a three-phase diode bridge firstly into proportional DC

voltage. Stabilization of the second DC link voltage is obtained with the buck type isolated DC/DC

converter by means of duty cycle variation. The main drawback of this solution is high currents in the

transformer’s primary winding at rated wind speeds that will reduce converter efficiency at this operating

point. In the second concept of inverter topologies have proposed a one-phase soft-switched dual LCL

DC/AC converter (Fig. 9b). This converter utilizes a controlled rectifier for generator voltage

rectification and DC link voltage stabilization. The soft-switched dual LCL DC/AC converter needs

stable DC link voltage, so generator voltage should be boost up to its maximum voltage amplitude value

in the whole input voltage range that will reduce the efficiency of the controlled rectifier at low generator

speed.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

(a)

(b)

Fig. 9. Interfacing converter topologies: a) with a buck type isolated DC/DC converter, b) one-

phase LCL DC/AC converter

NEW PROPOSED TOPOLOGY

To improve the efficiency of the PMSG based VSWT system a new converter topology is

introduced, presented in Fig. 10. It consists of a three-phase full bridge controlled rectifier (generator side

inverter) with PFC functionality and a quasi-Z-source (qZS) DC/DC converter with an HF transformer

for galvanic isolation. Grid side inverters with Output filters are not discussed here.

Fig 10. proposed interface converter with qZS DC/DC.

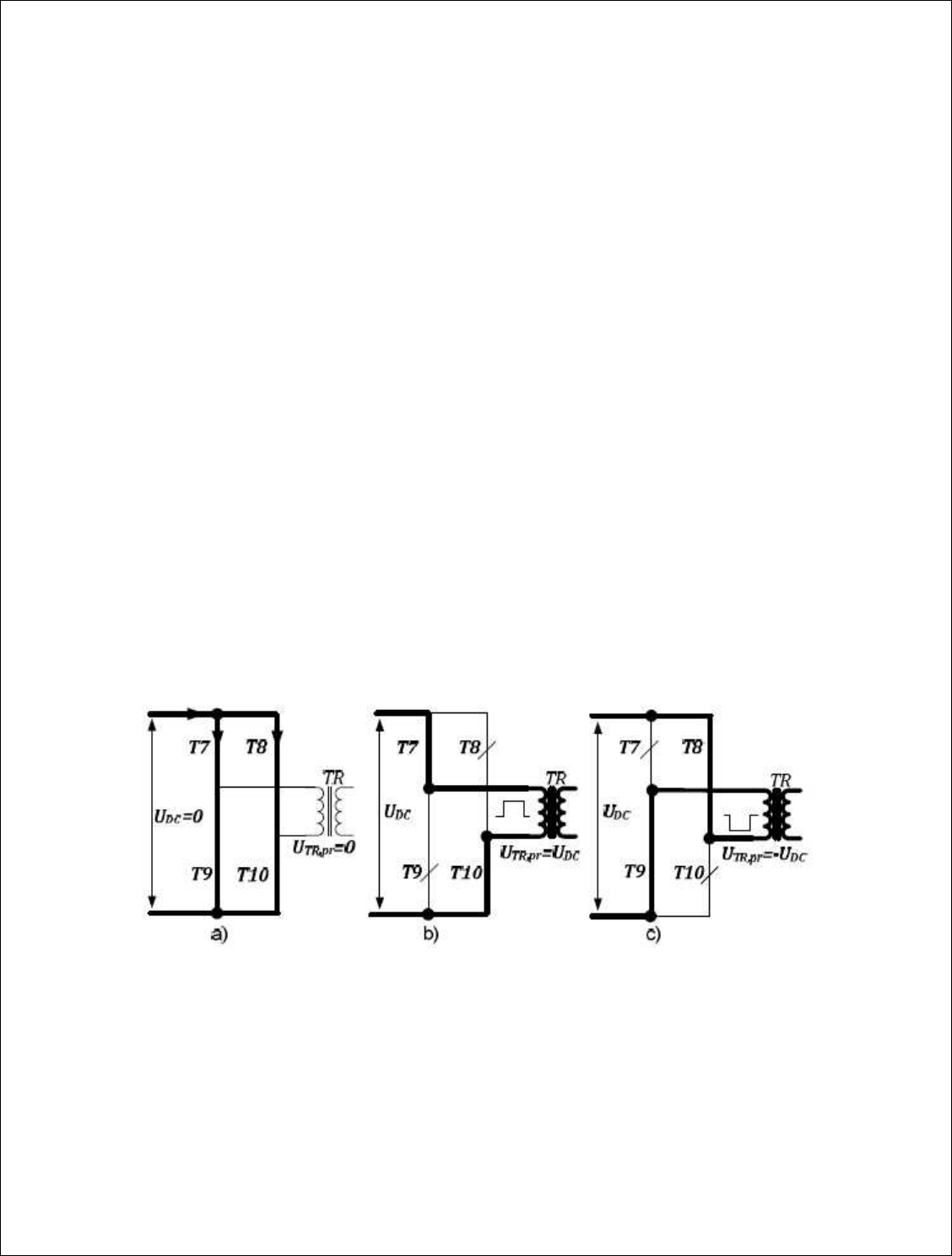
ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

A PFC inverter converts the variable voltage with variable frequency Ugen from the PMSG into a

stabilized DC voltage U

dc1

. The qZS DC/DC converter offers galvanic isolation and voltage level

adjustment by means of the transformation coefficient. The unique qZS impedance network and

appropriate control offer an additional voltage regulation capability at high efficiency. Stabilized DC link

voltage Uout can be inverted into the grid current by an appropriate inverter.

QZS BASED STEP-UP DC/DC CONVERTER WITH HF ISOLATION

The central idea implemented in the proposed converter is to keep the intermediate DC link

voltage (U

) constant despite the variation of the generator side DC link voltage U

DC1

. By keeping the

constant the inverter could be operated with a fixed duty cycle, thus ensuring constant volt-second

and flux swing of the isolation transformer.

The main advantage of the implemented quasi-Z-source (qZS) based step-up DC/DC converter is

that it can boost the input voltage during special shoot-through op erating states of the inverter. During

the shoot-through states the primary winding of the isolation transformer is shorted through all switches

of both phase legs of the inverter (Fig. 11a). The passive qZS-network makes the shoot-through states

possible, effectively protecting the circuit from damage. Moreover, the shoot-through states are used to

boost the magnetic energy stored in the inductors L

and L

without short-circuiting capacitors C

and C

This increase in the magnetic energy in turn provides the boost of voltage seen on the inverter output

during the active states of the inverter (Figs. 11b and 11c). Thus, by adjusting the shoot-through duty

cycle DS of the inverter twitches T

…T

the U

could be pre regulated to the desired 250 V despite the

variation of U

DC1

with different wind speeds from 150 V to 250 V (Fig.12).After the preregulation of U

the isolation transformer TR is being supplied from the inverter with a voltage of constant amplitude (250

V) and duty cycle (DA=0.4).

Fig 11. Inverter equivalent scheme during the shoot-through state (a) and during active states: positive

(b) and negative (c) half-cycles.

To reduce the turns ratio of the isolation transformer a voltage doubler rectifier (VDR) was

implemented on the secondary side of the converter. In contrast to the traditional full-bridge rectifier, two

diodes of one leg in the VDR topology were replaced by the capacitors. The operation principle of the

VDR is explained in Figs.12. During the positive half cycle, the capacitor C

is charged through the diode

to the peak secondary voltage of the isolation transformer (Fig. 12a). During the negative half cycle

the capacitor C

is charged through diode D3 (Fig. 12b). At every time instant the output voltage (U

DC2

)

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

from this circuit will be the sum of the two capacitor voltages ,or twice the peak voltage (U

TR,sec

) of the

secondary winding of the isolation transformer.

Fig 12. Operation principle of VDR: positive (a) and negative (b) half cycles.

OPERATING MODES OF NEW INTERFACING CONVERTER

This research attempts to prove the ability of the proposed topology to ensure stable grid side DC

link voltage U

out

. For this reason only the operating studied in more detail. The power circuit of the qZS

based DC/DC converter is shown in Fig. 10, but operation modes in Fig. 13.

Fig 13.operating modes of converter

The voltage boost necessary is obtained by two steps. The PFC rectifier stabilizes the first DC link

voltage U

dc1

to a 150V level when the generator voltage is below 112V

The controlled rectifier works as a usual rectifier when the generator voltage U

gen

is above 112V.

In this mode the DC link voltage is changed proportionally to the generator voltage, at the range from

150V in rated speed conditions up to 250V at the maximal speed.

The qZS based HF isolation converter is stabilizing the HF inverter input voltage U

to 250V

despite the voltage variations on the first DC link. The stabilized input voltage U

ensures inverter

operation with the fixed duty cycle, thus ensuring constant volt second balance of the isolation

transformer. The input voltage U

regulation is obtained by changing the shoot-through duty cycle

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

PERMANENT MAGNET SYNCHRONOUS MACHINE

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

OUTPUT:

(1)

is_abc(A)

(2)

we(rad/s)

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

(3)Te(Nm)

RESULT:

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

EXPNO:9 DATE:

COMPUTATION OF HARMONIC INDICES GENERATED BY A RECTIFIER FEEDING A

R-L LOAD

AIM:

To perform the harmonic analysis of single phase full bridge converter with R-L load

using Matlab (Simulink).

SOFTWARE REQUIRED:

Power system module of MATLAB

THEORY

HARMONICS:

There are certain loads on the system that produce harmonic currents. These currents result in

distorted voltages and currents that can adversely impact the system performance in different ways.

Generally this load is called as non linear load. The current wave shape on a non-linear load is not the

same as the voltage as shown in fig2.

Fig 1:-Voltage and Current waveforms for non-linear loads

Typical examples of non-linear loads include rectifiers (power supplies, UPS units, discharge

lighting), adjustable speed motor drives, ferromagnetic devices, DC motor drives and arcing

equipment. The current drawn by non-linear loads is not sinusoidal but it is periodic, meaning that the

current wave looks the same from cycle to cycle. Periodic waveforms can be described mathematically

as a series of sinusoidal waveforms that have been summed together as shown in fig 3.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Fig 2:-Waveform with symmetrical harmonic components

The sinusoidal components are integer multiples of the fundamental where the fundamental.

The only way to measure a voltage or current that contains harmonics is to use true-RMS reading

meter. If an averaging meter is used, which is the most common type, the error can be significant.

HARMONIC ANALYSIS:

Harmonic analysis is the branch of mathematics that studies the representation of functions or

signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series

and Fourier transforms. The basic waves are called "harmonics", hence the name "harmonic analysis".

RECTIFIER:

DEFINITION: Converting AC (from mains or other AC source) to DC power by using power diodes

or by controlling the firing angles of thyristors /controllable switches.

BASIC BLOCK DIAGRAM:

•Input can be single or multi-phase (e.g. 3-phase).

•Output can be made fixed or variable.

EXERCISE:

A single phase AC source of 230V, 50Hz supplying to a RL branch through a full bridge

converter connected using IGBT. The pulse trigger given to the IGBT is of amplitude 2 for a period

0.02 seconds with a period of 50% period. Deign a harmonic filter for 2 cycles and obtain the

necessary wave form.

ALGORITHM:

Step1: Start.

Step2: Obtain various blocks from simulink library and construct the block diagram of the converter.

Step3: Perform FFT analysis for the above.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Step4: Extract the harmonics.

Step5: Stop.

FLOW CHART:

Simulation diagram for THD voltage:

Start

Form the various

Simulink blocks

Perform FFT analysis for

the above

Extract the

harmonics

Start

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

OUTPUT:

FFT Analysis:

RESULT:

Hence the harmonic analysis of a single phase full bridge converter using a RL branch is

simulated and its 3

and 5

harmonics are extrated.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

EX.NO:10 DATE:

DESIGN OF ACTIVE FILTER FOR MITIGATING HARMONICS

AIM:

To Design the active filter to improve power quality by mitigation harmonics

THEORY:

As the development of modern power electronics technology and the wider application of

various nonlinear devices, the current distortion makes increasingly serious pollution to the grid.

Therefore, harmonic current compensation has been drawn great attention.Active power filter is a new

type of power electronic device using for dynamic suppressing harmonics and compensating reactive

power. It can compensate harmonics with varying amplitude and frequency, and can overcome the

shortage of passive filter effectively. It is a harmonics suppression device with prospect .

In 1980’s, with the self turn-off power semiconductor appeared, PWM control technology and

the instantaneous reactive power theory for three-phase system put into use, study on active power

filter become fast.Because of extensive use for three-phase four-wire in power system, such as

industry, official and business, many people pay more attention to the trouble which is caused by

harmonics and unbalance of three-phase. Therefore, it is important to compensate harmonics and

reactive power in three-phase four-wire system This paper introduces a shunt active power filter for

three-phase four-wire system. It presents the principles and structure. And the design and performance

of a 3KW experimental prototype is proposed.

PRINCIPLE AND STRUCTURE:

The structure of a shunt active power filter used for three-phase four-wire is shown in Fig. 1. In this

system, the load may product harmonics and unbalance current in three-phase, and current is flown in

neutral wire.

Fig. 1: The structure of active power filter for three-phase four-wire system

The shunt active power filter is a voltage source inverter controlled as a current source by means of

pulse width modulation signals. As it can be seen in Fig. 1, the filter is connected in paralleled with

the nonlinear load. Harmonic current compensation is achieved by injecting equal but opposite

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

harmonic current components at the point of connection, therefore canceling the original distortion

and improving the power quality . In most cases, the load also needs reactive power, which can also be

generated by the same current source. In three-phase unbalanced and nonlinear loads, it is also

possible to redistribute power and to keep the system balance. The active power filter is composed of

the reference current calculating circuit, current tracking circuit, driving circuit and the main circuit.

While, the generation circuit of compensating current is composed of the last three parts Three-phase

four-wire system is different from three-phase three-wire system because of the neutral wire. Thus,

handling zero-sequence components of three-phase current is the key point. Reference current

calculating circuit should product the reference current correctly and fast in three-phase four-wire

system. That means it should detect the harmonics, fundamental negative-sequence current

components and zero-sequence current components of the compensating . The generation circuit of

compensating current should product compensating current correctly according to the reference

current signals.

Because the sum of three-phase current is not zero in three-phase four-wire system, the detection

method based on instantaneous reactive power theory should be modified. The way is to calculate the

zero-sequence current components, then subtract them from three-phase current. Finally three-phase

current without zero-sequence components can be detected by the method based on instantaneous

reactive power theory. The compensating current signals of the neutral wire can be also calculated by

turning the polarity of the neutral wire current over . The principle of reference current calculating

circuit is shown in Fig. 2. In which,

cba

iii ,,

are load currents. The zero-sequence component of three-

phase current

is calculated as:

)(

cban

iiii 

(1)

Then zero-sequence components can be subtracted from three-phase current:

ncc

nbb

naa

iii



(2)

Eventually the three-phase currents without zero-sequence component

'''

cba

iii

will comply with:

'''



cba

iii

(3)

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Fig. 2: The principle diagram of reference current calculating circuit

Afterward, as shown in Fig. 2, the three-phase currents without zero-sequence components

'''

cba

iii

are

coordinately transformed and achieve corresponding active power current component i

and reactive

power current component i

, then it can acquire dc component

ii ,

through the low pass filters.

Fundamental positive-sequence components

'''

cfbfaf

iii

can be calculated by inverse coordinate

transformation. When the positive-sequence components are subtracted from load current i

, there

will be reference current i

. After the compensating currents generated by the reference

signals offset the harmonics, the currents flowing into source which are equal to fundamental positive-

sequence components are sinusoid and balanced

DESIGN OF SHUNT ACTIVE POWER FILTER

Active power filter is an advanced power electronic device, which can be used for integrated

compensating harmonics, reactive currents and negative-sequence currents. Because of the

characteristics of real time and accurate compensation, it is possible to take full advantage of digital

signal processing and many other technologies. If so, the performance of active power filters can be

improved significantly.

Control circuit

The control circuit consists of current control and voltage control. The principle is shown in Fig. 3.

The current controller uses the current error between reference current

and compensating

current

filtered by a proportional-integral regulator as the modulating signal. The current control

circuit uses a tracking PWM current control and timing comparing. The comparator is judged at each

clock-cycle, so the PWM control signals change once at least one clock cycle. The clock-cycle limits

the highest frequency of switching devices in the main circuit, thus damages to the devices due to

over-high switching frequency may be avoided. The shortcoming of this control method is that the

tracking error of compensating current is unfixed .

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

For voltage control, it mainly means controlling of DC-link voltage. There are two control techniques:

PI control and fuzzy control. PI control is similar to the current control, but there is some difference.

When the supply voltage is unbalanced or distorted, the input of the voltage controller is not the actual

supply voltage but a unitary sinusoidal waveform in phase with the supply voltage . Therefore, the

active power filter will have good performance even under the condition of unbalanced or distorted

source voltage. In other words, PI control uses the voltage error between DC-link voltage and its

reference filtered by a proportional-integral regulator multiplied by the unitary sinusoidal waveform in

phase with the supply voltage to obtain the reference current.

fig. 3: The principle diagram of control circuit

Fuzzy control can be also applied to DC-link voltage control. The input of the controller is the error

voltage and its incremental variation. And the output is the incremental variation of the amplitude of

the active current injected into active power filter. Compared with PI control, fuzzy control has better

dynamic response and can keep the DC-link voltage stability well. However, fuzzy control makes the

controller complicated. This paper adopts PI control as control method.

Main circuit

In three-phase four-wire system, active power filter not only compensates the harmonics of three-

phase current, but also suppresses the current of neutral wire to get rid of the neutral wire current of

the source. There are many methods to suppress the neutral current. Generally, four-leg converter and

three-leg converter are commonly used . The structures of their main circuit are shown respectively in

Fig. 4 and Fig. 5.For four-leg structure, to compensate the neutral current is provided through the forth

leg which products the compensating current of the neutral wire, which offset the neutral current of the

source side. The compensating principle of this method is easy, but it makes the circuit more

complicated and the cost is high. In this paper, the main circuit uses three-leg converter. Through

reference current calculating circuit, it can acquire reference current signals of compensating three-

phase currents and the neutral current. The compensating current of three-phase currents is equal to the

sum of harmonics, fundamental negative-sequence and zero-sequence components in load current

which offsets the load current. So the supply current flowing into the source which is equal to the

fundamental positive-sequence components becomes sinusoidal and balanced. For three-leg structure,

to keep the DC-link voltage balance is to control the neutral current to be zero . From the point of

active power filter, the sum of harmonics and fundamental negative-sequence components of three-

phase current without zero-sequence components is aero. The sum of zero-sequence components of

three-phase current is equal to the compensating neutral current which is regulated through DC-link

control.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

Nonlinear load

icn

VTn1

VTn2

Udc

Fig. 4: The four-leg structure of main circuit

Fig. 5: The three-leg structure of main circuit

After compensation of active power filter, the three-phase supply current will be sinusoidal and

balanced, the neutral current of the source will be zero.

A 3kW shunt three-phase four-wire active power filter experimental prototype is constructed. Firstly,

the minimum DC-link voltage U

should be greater than the value three times of AC phase peak

voltage E

. If DC-link voltage is too small, compensation current can not track instruction current as

requests, and the compensation effect will be unsatisfied. On this basis, the greater Uc is, the faster i

changes, the higher voltage the devices should endure . Secondly, the smaller inductance L is, the

faster i

changes. Thirdly, the longer current controlling cycle t

is, the greater ripple current tracking

error has. The value of t

also determines the highest time of harmonic which the active power filter

can compensate and the frequency demands for switching devices.

The work process of active power filter is also the process of capacitor charging and discharging. The

fluctuation of DC-link voltage can be explained by the changes of the stored charges volume, and the

volume can be obtained from the integral of current to time. According to the parameters design

method for capacitance in and , the capacitor C under ideal condition can be calculated by equation

(4)

,

where C is capacitor value; Q is the electric charges stored on capacitor; u is reference capacitor

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

voltage; Q

is the maximal charge,

uu \

is the maximal voltage fluctuation; i

is compensating

current of phase a; i is fundamental active current; I

is load current.





















)6/sin(*2

3/2









tiii

tdiQ

C. Driving circuit

IGBT is used as switching device in this system. The IGBT driving circuit uses the driving block

M57962L produced by MITSUBISHI company in Japan. This drive block is a mix integrated circuit.

Because of gathering the drive and over-current protecting circuit, it can satisfy the needs perfectly.

EXPERIMENT RESULTS

According to the design described above, a 3 KW experimental prototype of shunt active power filter

for three-phase four-wire system is developed. The experiment results are given in Fig. 6 and Fig. 7.

The nonlinear load is composed of the inductance three-phase transistor rectifier bridge. Fig. 6 is the

waveform of the supply current before using the active power filter. It is three-phase unbalanced and

distorted current source. Fig. 7 is the waveform of the supply current after compensation, and it is

three-phase balanced and sinusoidal current. This indicates that the proposed active power filter has a

good performance and the design method is basically correct.

Fig. 6: Three-phase currents before compensation

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

100

Fig. 7: Three-phase currents after compensation

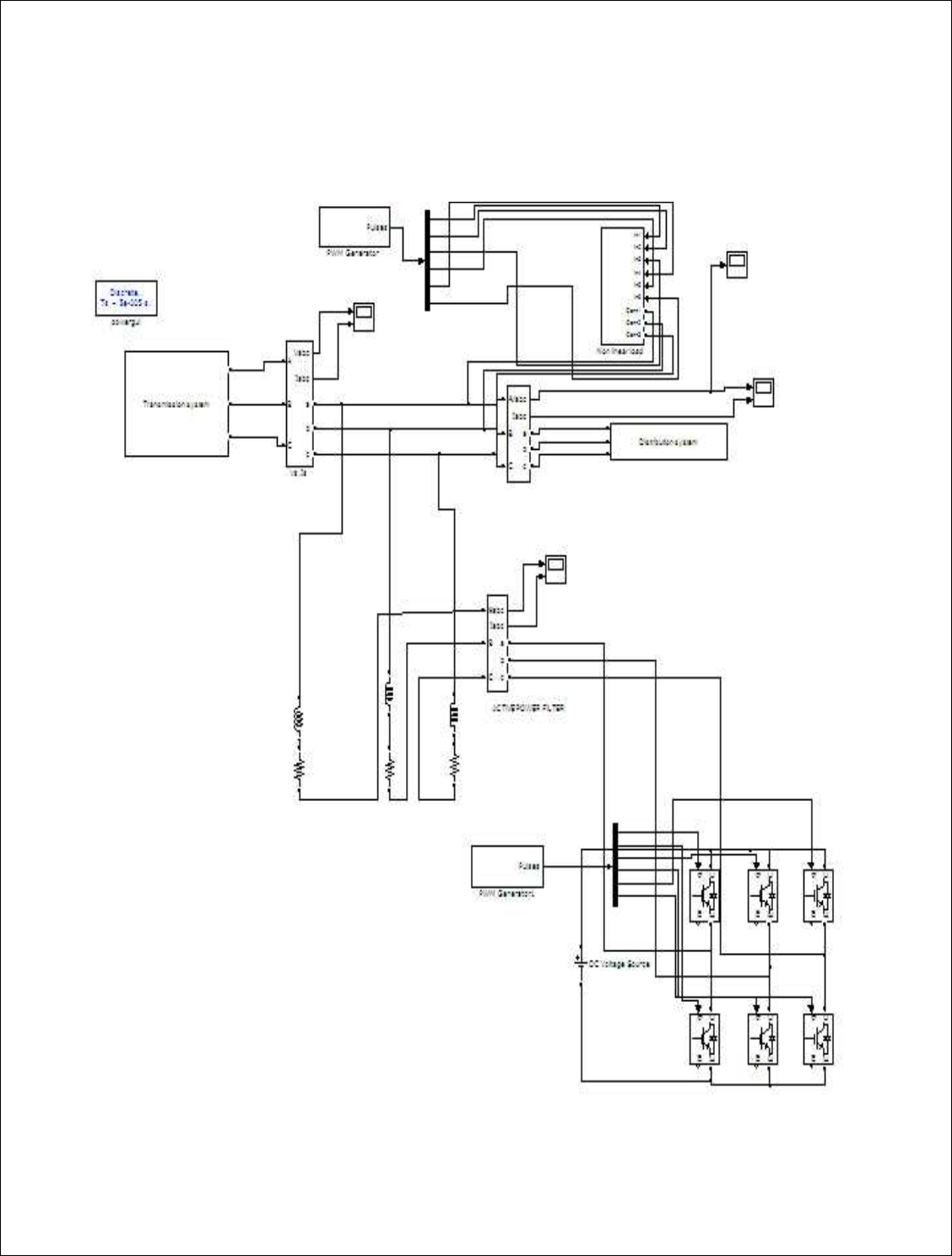
ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

101

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

102

RESULT: Thus the active filter for mitigation harmonics was designed

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

103

EXP NO: 11 DATE:

TRANSIENT STABILITY ANALYSIS: SINGLE MACHINE

INFINITE BUS SYSTEM USING CLASSICAL MODEL

AIM

To become familiar with various aspects of the transient stability analysis of Single

Machine Infinite Bus (SMIB) system.

OBJECTIVE

To understand modeling and analysis of transient stability of a SMIB power system.

SOFTWARE REQUIRED

TRANSIENT - SMIB module of AU Power lab or equivalent.

THEORY

Stability

Stability problem is concerned with the behavior of power system when it is subjected

to disturbances and is classified into small signal stability problem if the disturbances are small

and transient stability problem when the disturbances are large.

Transient Stability

When a power system is under steady state, the load plus transmission loss equals to the

generation in the system. The generating units run at synchronous speed and system frequency,

voltage, current and power flows are steady. When a large disturbance such as three phase fault,

loss of load, loss of generation etc., occurs the power balance is upset and the generating units

rotors experience either acceleration or deceleration. The system may come back to a steady state

condition maintaining synchronism or it may break into subsystems or one or more machines

may pull out of synchronism. In the former case the system is said to be stable and in the later

case it is said to be unstable.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

104

SINGLE MACHINE- INFINITE BUS SYSTEM

OUTPUT

Case 1: Opening & Closing of Circuit Breaker at line-2

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

105

Case 2: Three-phase to ground fault at the mid point of line-2

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

106

Case 3: Three-phase to ground fault at the end of line-2

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

107

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

108

RESULT:

Thus the transient stability of a Single-Machine Infinite Bus(SMIB) System was analyzed &

output graphs for different cases were obtained.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

109

EXP NO: 12 DATE:

SMALL SIGNAL STABILITY ANALYSIS OF A SINGLE MACHINE INFINITE BUS

SYSTEM WITH FIELD CIRCUIT, EXCITER AND POWER SYSTEM STABILIZER

AIM:

To write a MATLAB program for analyzing the small signal stability of a single machine infinite

bus system with field circuit, exciter and power system stabilizer.

SOFTWARE REQUIRED:

Power system module of MATLAB.

THEORY:

Effect of Synchronous Machine Field Circuit Dynamics:

We now consider the system performance including the effect of field flux variations. The

amortisseur effects will be neglected and the field voltage will be assumed constant (manual

excitation control).

Synchronous machine equations:

As in the case of the classical generator model, the acceleration equations are

(1)

where

Network equations:

The machine terminal and infinite bus voltages in terms of the d and q components are

t d q

E = e + je

(2)

B Bd Bq

E = E + jE

(3)

The network constraint equation for the system

 

t B E E t

E = E + R + jX I

% % %

(4)

   

 

d q Bd Bq E E d q

e + je = E + jE + R + jX i + ji

(5)

Resolving into d and q components gives

d E d E q Bd

e = R i - X i + E

(6)

q E q E d Bq

e = R i + X i + E

(7)

Where,

Bd B

E = E sin

(8)

Bq B

E = E cos

(9)

The expressions for i

and i

in terms of the state variables ψ

and δ is given by

 

 

 

 

 

 

ads

Tq fd B T B

ads fd

ψ -E cosδ -R E sinδ

L + L

i =

(10)

 

r m e D r

0 r

Δω = T -T -K Δω

δ = ω Δω

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

110

 

 

 

 

 

 

ads

T fd B Td B

ads fd

ψ -E cosδ + X E sinδ

L + L

i =

(11)

T a E

R = R + R

(12)

 

Tq E aqs l E qs

X = X + L + L = X + X

(13)

 

 

Tqd E ads l E ds

X = X + L + L = X + X

(14)

T Tq Td

D = R + X X

(15)

The reactance’s L

ads

and L

aqs

are saturated values. In per unit they are equal to the

corresponding inductances.

These equations are nonlinear and have to be linearized for small signal analysis.

Linearized system equations

Expressing equations (11) and (13) in terms of perturbed values, we may write

d 1 2 fd

Δi = m Δδ +m Δψ

(16)

q 1 2 fd

Δi = n Δδ +n Δψ

(17)

 

B Tq 0 T 0

E X sin

δ - R cosδ

m =

(18)

 

B T 0 Td 0

E R sin

δ + X cosδ

n =

(19)

 

T¶q

ads

ads fd

m =

D L +L

(20)

 

ads

ads fd

n =

D L + L

(21)

By linearizing ψ

and ψ

, and substituting them in the above expressions and , we get

 



 

 

ad ads d

Δψ

Δψ = L -Δi +

(22)

 

 

 

 

2 ads fd 1 ads

= -m L

Δψ -m L Δδ

(23)

aq aqs q

Δψ = -L Δi

(24)

2 aqs fd 1 aqs

= -n L

Δψ -n L Δδ

(25)

Linearizing i

and substituting for

∆ψ

from equation (19) gives

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

111

fd ad

Δψ -Δψ

Δi =

(26)

 



 

 

 

ads

ads fd 1 ads

fd fd fd

1 1

= 1- + L

Δψ + m L Δδ

L L L

(27)

The linearized form of air gap torque

is given by

e ad0 q q0 ad aq0 d d0 aq

ΔT = ψ Δi + i Δψ - ψ Δi -i Δψ

(28)

e 1 2 fd

ΔT = K Δδ + K Δψ

(29)

   



1 1 ad0 aqs d0 1 aq0 ads q0

K = n

ψ + L i -m ψ + L i

(30)

   



ads

2 2 ad0 aqs d0 2 aq0 ads q0 q0

K = n

ψ +L i -m ψ + L i + i

(31)

The system equation in the desired final form :

 

 

 

11 12 13

fd 32 33 fd

Δω

a a a

Δδ = a 0 0 Δδ

Δψ 0 a a Δψ

(32)

Where,

a = -

(33)

a = -

(34)

a = -

(35)

21 0 0

a =

ω = 2πf

(36)



0 fd

32 1 ads

ω R

a = m L

(37)

 



 

 

0 fd ads

33 2 ads

fd fd

ω R L

a = - 1- + m L

L L

(38)

b =

(39)

and

ΔT

and

ΔE

depend on prime mover and excitation controls. With constant mechanical

input torque,

ΔT

=0; with constant exciter output voltage,

ΔE

=0.

0 fd

adu

ω R

b =

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

112

Summary of procedure for formulating the state matrix

(a)The following steady state operating conditions , machine parameters and network parameters

are given below:

sat

Alternatively E

may be specified instead of Q

or E

(b)The first step is to compute the initial steady state values of system variables:

, power factor angle ,Total saturation factors K

and K

ds ds sd adu l

X = L = K L + L

(40)

qs qs sq aqu l

X = L = K L + L

(41)

 

 

 

t qs t a

-1

t t a t qs

I X cosj-I R sinj

δ = tan

E + I R cosj+ I X sinj

(42)

d0 t i

e = E sin

(43)

q0 t i

e = E cos

(44)

 

d0 t i

i = I sin

δ + j

(45)

 

q0 t i

i = I cos

δ + j

(46)

Bd0 d0 E d0 E q0

E = e - R i + X i

(47)



0 fd

32 1 ads

ω R

a = m L

(48)

 

 

 

-1

Bdo

Bq0

δ = tan

(49)





2 2

Bdo Bqo

1/2

E = E + E

(50)

q0 a q0 ds d0

fd0

ads

e + R i L i

i = ,

(51)

fd0 adu fd0

E = L i

(52)

 

ad0 ads d0 fd0

ψ = L -i +i

(53)

(54)

(c)The next step is to compute incremental saturation factors and the

corresponding saturated values of L

ads

aqs ,

L’

ads

, and then

T Tq Td

R ,X ,X ,D

aq0 aqs q0

ψ = -L i

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

113

1 2 1 2

m ,m ,n ,n

1 2

K ,K

is calculated from the equations (11) and (14).

(d) Finally, compute the elements of matrix A.

Block diagram representation

Fig.1 shows the block diagram representation of the small signal performance of the system .In

this representation, the dynamic characteristics of the system are expressed in terms of the so

called K constants. The basis for the block diagram and the expressions for the associated

constant are developed .

Fig.1-BLOCK DIAGRAM REPRESENTATION WITH CONSTANT E

EFFECTS OF EXCITATION SYSTEM:

We will examine the effect of the excitation system on the small signal stability performance of

the single machine infinite bus system.

The input control signal to the excitation system is normally the generator terminal voltage E

. In

the generator model E

is not a state variable. Therefore, E

has to be expressed in terms of the

state variables Δ ω

, Δδ, and



May be expressed in complex form:

t d q

E = e + je

(55)

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

114

Hence,

2 2 2

t d q

E = e +e

(56)

Applying a small perturbation, we may write

2 2 2

t0 t d0 d q0 q

(E +

ΔE ) = (e +Δe ) +(e +Δe )

(57)

By neglecting second order terms involving perturbed values , the above equation reduces to

t0 t d0 d q0 q

ΔE = e Δe + e Δe

(58)

Therefore,

t d q

t0 t0

ΔE = Δe + Δe

E E

(59)

In terms of the perturbed values, Equations

d a d l q aq

q a q l d ad

Δe = -R Δi +L Δi -Δψ

(60)

Use of Equations to eliminate

d q ad

Δi ,Δi ,Δψ

and



from the above equations in terms of the

state variables and substitution of the resulting expressions for

e

and

e

in equation yield

t 5 6 fd

ΔE = K Δδ+K Δψ

(61)

Where

5 a 1 l 1 aqs 1 a 1 l 1 ads 1

t0 t0

K = [-R m +L n +L n ]+ [-R n -L m -L m ]

E E

(62)

6 a 2 l 2 aqs 2 a 2 l 2 ads 2

t0 t0 fd

K = [-R m +L n +L n ]+ [-R n -L m +L ( -m )]

E E L

(63)

Fig.2 THYRISTOR EXCITATION SYSTEM WITH AVR

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

115

34 32 A

a = -b K

a = 0

a =

a = -

(64)

The complete state space model for the power system , including the excitation system is given

 

 

 

11 12 13

32 33 34 fd

42 43 44

Δω

a a a 0

a 0 0 0

Δδ

= +

ΔT

0 a a a

Δψ

0 a a a

Δν

(65)

Block diagram including the excitation system:

Fig 3- BLOCK DIAGRAM REPRESENTATION WITH EXCITER AND AVR

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

116

POWER SYTEM STABILIZER:

The basic function of a power system stabilizer (PSS) is to add damping to the generator

rotor oscillations by controlling its excitation using auxiliary stabilizing signal(s). To provide

damping, the stabilizer must produce a component of electrical torque in phase with the rotor

speed deviations.

The theoretical basis for a PSS may be illustrated with the aid of the block diagram

shown below.

Since the purpose of a PSS is to introduce a damping torque component, a logical signal

to use for controlling generator excitation is the speed deviation Δ

ωr

If the exciter transfer function G

(s) and the generator transfer function between ΔE

and

were pure gains, a direct feedback of Δ

ωr

would result in a damping torque component.

However, in practice both the generator and the exciter (depending on its type) exhibit frequency

dependent gain and phase characteristics. Therefore, the PSS transfer function, GPSS(s), should

have appropriate phase compensation circuits to compensate for the phase lag between the

exciter input and the electrical torque. In the ideal case, with the phase characteristics of

GPSS(S) being an exact inverse of the exciter and generator phase characteristics to be

compensated, the PSS would result in a pure damping torque at all oscillating frequencies.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

117

Fig 4- BLOCK DIAGRAM REPRESENTATION WITH AVR AND PSS.

The PSS representation in figure shown below consists of three blocks: a phase

compensation block, a signal washout block, and a gain block.

Fig 5- THYRISTOR EXCITATION SYSTEM WITH AVR AND PSS

System state matrix including PSS

51 STAB 11

52 STAB 12

53 STAB 13

61 51

62 52

63 53

1 1

65 55

2 2

0 fd

36 A

adu

a = K a

a = -

a = a

T T

a = a +

T T

ω R

a = K

(66)

The complete state space model, including the PSS, has the following form

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

118

 

 

 

11 12 13

32 33 34 36

42 43 44

51 52 53 55

61 62 63 65 66

Δω

a a a 0 0 0

Δδ

a 0 0 0 0 0

Δδ

Δψ

0 a a a 0 a

Δψ

0 a a a 0 0

Δν

a a a 0 a 0

Δν

a a a 0 a a

Δν

(67)

RESULT:

A MATLAB program was written to analyze the small signal stability of single machine infinite

bus system with field circuit, exciter and power system stabilizer.

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

119

PROGRAM FOR SMALL SIGNAL STABILITY ANALYSIS OF SINGLE MACHINE

INFINITE BUS SYSTEM

1. WITH FIELD CIRCUIT

p=0.9;q=0.3;Et=1;h=3.5;xd=1.81;xq=1.76;xdp=0.3;x1=0.16;Ra=0.003;Tdop=8;Ladu=1.65;Laqu

=1.60;L1=0.16;Rfd=0.0006;

Xtr=0.15;x1=0.5;ksd=0.8491;ksq=0.8491;x2=0.93;Re=0;Lfd=0.153;kd=0;fo=60;

Xe=Xtr+x1;

s=p+q*i;

It=s'/Et';

phi=atan(q/p);

Lds=(ksd*Ladu)+L1;

Lqs=(ksq*Laqu)+L1;

Xqs=Lqs;

Xds=Lds;

a=(abs(It)*Xqs*cos(phi)-abs(It)*Ra*sin(phi));

b=(Et+(abs(It)*Ra*cos(phi))+(abs(It)*Xqs*sin(phi)));

deli=atan(a/b);

edo=Et*sin(deli);

eqo=Et*cos(deli);

ido=abs(It)*sin(deli+phi);

iqo=abs(It)*cos(deli+phi);

Ebdo=edo-(Re*ido)+(Xe*iqo);

Ebqo=eqo-(Re*iqo)-(Xe*ido);

delo=atan(Ebdo/Ebqo);

Ep=sqrt(Ebdo^2+Ebqo^2);

Lads=Lds-L1;

Laqs=Lqs-L1;

ifdo=(eqo+(Ra*iqo)+(Lds*ido))/Lads;

Efdo=Ladu*ifdo;

siado=Lads*(-ido+ifdo);

siaqo=-Laqs*iqo;

Rt=Ra+Re;

Xtq=Xe+(Laqs+L1);

Ladsp=1/(inv(Lads)+inv(Lfd));

Xtd=Xe+(Ladsp+L1);

D=(Rt^2)+(Xtq*Xtd);

m1=(Ep*(Xtq*sin(delo))-(Rt*cos(delo)))/D;

n1=(Ep*(Rt*sin(delo))+(Xtd*cos(delo)))/D;

m2=(Xtq*Lads)/(D*(Lads+Lfd));

n2=(Rt*Lads)/(D*(Lads+Lfd));

k1=n1*(siado+(Lads*ido))-m1*(siaqo+(Ladsp*iqo));

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

120

k2=n2*(siado+(Laqs*ido))-m2*(siaqo+(Ladsp*iqo))+((Ladsp/Lfd)*iqo);

a11=-kd/(2*h);

a12=-k1/(2*h);

a13=-k2/(2*h);

wo=2*pi*fo;

a21=wo;a22=0;a23=0;a31=0;

a32=(-wo*Rfd*m1*Ladsp)/Lfd;

a33=((-wo*Rfd)/Lfd)*(1-(Ladsp/Lfd)+(m2*Ladsp));

A=[a11 a12 a13;a21 a22 a23;a31 a32 a33];

lamda=eig(A);

c(1)=real(lamda(1));

d(1)=imag(lamda(1));

zeta=-c(1)/(sqrt(c(1)*c(1)+d(1)*d(1)));

ks=abs(Ep)*abs(Ep)*cos(delo)/(Xe+xdp);

wn=sqrt(-det(A));

wnhz=wn/(2*pi)

wd=wn*sqrt(1-zeta*zeta);

theta=acos(zeta);

Dd0=5*pi/180;

t=0:0.01:30;

Dd=Dd0/sqrt(1-zeta*zeta)*exp(-zeta*wn*t).*sin(wd*t+theta);

d=(delo+Dd)*180/pi;

plot(t,d)

xlabel('t sec'),ylabel('delta degrees')

OUTPUT:

0 5 10 15 20 25 30

t sec

delta degrees

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

121

2.WITH EXCITER

p=0.9;q=0.3;Et=1;h=3.5;xd=1.81;xq=1.76;xdp=0.3;x1=0.16;Ra=0.003;Tdop=8;Ladu=1.65;Laqu

=1.60;L1=0.16;Rfd=0.0006;

Xtr=0.15;x1=0.5;ksd=0.8491;ksq=0.8491;x2=0.93;Re=0;Lfd=0.153;kd=0;fo=60;Tr=.02;ka=0;

Xe=Xtr+x1;

s=p+q*i;

It=s'/Et';

phi=atan(q/p);

Ep=Et+xdp*It*i;

Lds=(ksd*Ladu)+L1;

Lqs=(ksq*Laqu)+L1;

Xqs=Lqs;

Xds=Lds;

a=(abs(It)*Xqs*cos(phi)-abs(It)*Ra*sin(phi));

b=(Et+(abs(It)*Ra*cos(phi))+(abs(It)*Xqs*sin(phi)));

deli=atan(a/b);

edo=Et*sin(deli);

eqo=Et*cos(deli);

ido=abs(It)*sin(deli+phi);

iqo=abs(It)*cos(deli+phi);

Ebdo=edo-(Re*ido)+(Xe*iqo);

Ebqo=eqo-(Re*iqo)-(Xe*ido);

delo=atan(Ebdo/Ebqo);

Ep=sqrt(Ebdo^2+Ebqo^2);

Lads=Lds-L1;

Laqs=Lqs-L1;

ifdo=(eqo+(Ra*iqo)+(Lds*ido))/Lads;

Efdo=Ladu*ifdo;

siado=Lads*(-ido+ifdo);

siaqo=-Laqs*iqo;

Rt=Ra+Re;

Xtq=Xe+(Laqs+L1);

Ladsp=1/(inv(Lads)+inv(Lfd));

Xtd=Xe+(Ladsp+L1);

D=(Rt^2)+(Xtq*Xtd);

m1=(Ep*(Xtq*sin(delo))-(Rt*cos(delo)))/D;

n1=(Ep*(Rt*sin(delo))+(Xtd*cos(delo)))/D;

m2=(Xtq*Lads)/(D*(Lads+Lfd));

n2=(Rt*Lads)/(D*(Lads+Lfd));

Eto=sqrt(edo*edo+eqo*eqo);

k1=n1*(siado+(Lads*ido))-m1*(siaqo+(Ladsp*iqo));

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

122

k2=n2*(siado+(Laqs*ido))-m2*(siaqo+(Ladsp*iqo))+((Ladsp/Lfd)*iqo);

k5=(-Ra*m1+L1*n1+Laqs*n1)*(edo/Eto)+(eqo/Eto)*(-Ra*n1-L1*m1-Ladsp*m1);

k6=(edo/Eto)*(-Ra*m2+L1*n2+Laqs*n2)+(eqo/Eto)*(-Ra*n2-L1*m2+Ladsp*(inv(Lfd)-m2));

a11=-kd/(2*h);

a12=-k1/(2*h);

a13=-k2/(2*h);

a14=0;

wo=2*pi*fo;

a21=wo;a22=0;a23=0;a31=0;a24=0;

a32=(-wo*Rfd*m1*Ladsp)/Lfd;

a33=((-wo*Rfd)/Lfd)*(1-(Ladsp/Lfd)+(m2*Ladsp));

a34=-wo*Rfd*ka*inv(Ladu);

a41=0;

a42=k5/Tr;

a43=k6/Tr;

a44=-inv(Tr);

A=[a11 a12 a13 a14;a21 a22 a23 a24;a31 a32 a33 a34;a41 a42 a43 a44];

lamda=eig(A);

c=real(lamda(3));

d=imag(lamda(3));

zeta=-c/(sqrt(c*c+d*d));

ks=abs(Ep)*abs(Ep)*cos(delo)/(Xe+xdp);

wn=sqrt(ks*wo/(2*h));

wnhz=wn/(2*pi)

wd=wn*sqrt(1-zeta*zeta);

theta=acos(zeta);

Dd0=5*pi/180;

t=0:0.01:10;

Dd=Dd0/sqrt(1-zeta*zeta)*exp(-zeta*wn*t).*sin(wd*t+theta);

d=(delo+Dd)*180/pi;

plot(t,d)

xlabel('t sec'),ylabel('delta degrees')

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

123

OUTPUT:

0 1 2 3 4 5 6 7 8 9 10

t sec

delta degrees

3.WITH POWER SYSTEM STABILIZER

p=0.9;q=0.3;Et=1;h=3.5;xd=1.81;xq=1.76;xdp=0.3;x1=0.16;Ra=0.003;Tdop=8;Ladu=1.65;Laqu

=1.60;L1=0.16;Rfd=0.0006;

Xtr=0.15;x1=0.5;ksd=0.8491;ksq=0.8491;x2=0.93;Re=0;Lfd=0.153;kd=0;fo=60;Tr=.02;ka=10;k

stab=48.5;Tw=1.4;T1=0.154;T2=.033;

Xe=Xtr+x1;

s=p+q*i;

It=s'/Et';

phi=atan(q/p);

Ep=Et+xdp*It*i;

Lds=(ksd*Ladu)+L1;

Lqs=(ksq*Laqu)+L1;

Xqs=Lqs;

Xds=Lds;

a=(abs(It)*Xqs*cos(phi)-abs(It)*Ra*sin(phi));

b=(Et+(abs(It)*Ra*cos(phi))+(abs(It)*Xqs*sin(phi)));

deli=atan(a/b);

edo=Et*sin(deli);

eqo=Et*cos(deli);

ido=abs(It)*sin(deli+phi);

iqo=abs(It)*cos(deli+phi);

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

124

Ebdo=edo-(Re*ido)+(Xe*iqo);

Ebqo=eqo-(Re*iqo)-(Xe*ido);

delo=atan(Ebdo^2+Ebqo^2);

Lads=Lds-L1;

Laqs=Lqs-L1;

ifdo=(eqo+(Ra*iqo)+(Lds*ido))/Lads;

Efdo=Ladu*ifdo;

siado=Lads*(-ido+ifdo);

siaqo=-Laqs*iqo;

Rt=Ra+Re;

Xtq=Xe+(Laqs+L1);

Ladsp=1/(inv(Lads)+inv(Lfd));

Xtd=Xe+(Ladsp+L1);

D=(Rt^2)+(Xtq*Xtd);

m1=(Ep*(Xtq*sin(delo))-(Rt*cos(delo)))/D;

n1=(Ep*(Rt*sin(delo))+(Xtd*cos(delo)))/D;

m2=(Xtq*Lads)/(D*(Lads+Lfd));

n2=(Rt*Lads)/(D*(Lads+Lfd));

Eto=sqrt(edo*edo+eqo*eqo);

k1=n1*(siado+(Lads*ido))-m1*(siaqo+(Ladsp*iqo));

k2=n2*(siado+(Laqs*ido))-m2*(siaqo+(Ladsp*iqo))+((Ladsp/Lfd)*iqo);

k5=(-Ra*m1+L1*n1+Laqs*n1)*(edo/Eto)+(eqo/Eto)*(-Ra*n1-L1*m1-Ladsp*m1);

k6=(edo/Eto)*(-Ra*m2+L1*n2+Laqs*n2)+(eqo/Eto)*(-Ra*n2-L1*m2+Ladsp*(inv(Lfd)-m2));

a11=-kd/(2*h);

a12=-k1/(2*h);

a13=-k2/(2*h);

wo=2*pi*fo;

a21=wo;

a32=(-wo*Rfd*m1*Ladsp)/Lfd;

a33=((-wo*Rfd)/Lfd)*(1-(Ladsp/Lfd)+(m2*Ladsp));

a34=-wo*Rfd*ka*inv(Ladu);

a36=wo*Rfd*ka*inv(Ladu);

a42=k5/Tr;

a43=k6/Tr;

a44=-inv(Tr);

a51=kstab*a11;

a52=kstab*a12;

a53=kstab*a13;

a55=-inv(Tw);

a61=T1*a51*inv(T2);

a62=T1*a52*inv(T2);

a63=T1*a53*inv(T2);

a65=T1*a55*inv(T2)+inv(T2);

a66=-inv(T2);

ADVANCE POWER SYSTEM SIMULATION LABORATORY (II SEM) ME

125

A=[a11 a12 a13 0 0 0;a21 0 0 0 0 0;0 a32 a33 a34 0 a36;0 a42 a43 a44 0 0;a51 a52 a53 0 a55

0;a61 a62 a63 0 a65 a66];

lamda=eig(A);

c=real(lamda(4));

d=imag(lamda(4));

zeta=-c/(sqrt(c*c+d*d));

ks=abs(Ep)*abs(Ep)*cos(delo)/(Xe+xdp);

wn=sqrt(ks*wo/(2*h));

wnhz=wn/(2*pi)

wd=wn*sqrt(1-zeta*zeta);

theta=acos(zeta);

Dd0=5*pi/180;

t=0:0.01:10;

Dd=Dd0/sqrt(1-zeta*zeta)*exp(-zeta*wn*t).*sin(wd*t+theta);

d=(delo+Dd)*180/pi;

plot(t,d)

xlabel('t sec'),ylabel('delta degrees')

OUTPUT:

0 1 2 3 4 5 6 7 8 9 10

t sec

delta degrees